46. In the propped cantilever beam carrying a uniformly distributed loaf of w N/m, shown in the following figure, the reaction at the support B is
    

1. 1. 5/8 wL

   
   
   

   2. 3/8 wL

   
   
   

   3. 1/2 wL

   
   
   

   4. 3/4 wL

   
   
   

---

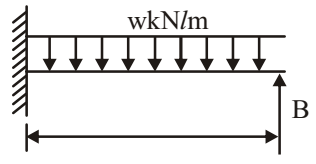
1. View Hint View Answer Discuss in Forum

   	wL4	=	RBL3
   	8EI		3EI

   
   

   ⇒ RB =	3	wL
   	8

   Correct Option: B

   	wL4	=	RBL3
   	8EI		3EI

   
   

   ⇒ RB =	3	wL
   	8

---

47. A bar of varying square cross-section is loaded symmetrically as shown in the figure, loads shown are placed on one of the axes of symmetry of cross-section. Ignoring self weight, the maximum tensile stress in N/nm² anywhere is
    

1. 1. 16.0

   
   
   

   2. 20.0

   
   
   

   3. 25.0

   
   
   

   4. 30.0

   
   
   

---

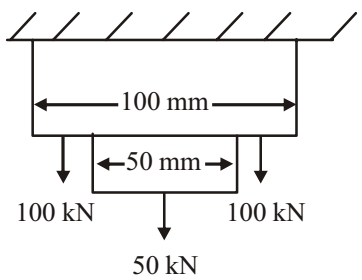
1. View Hint View Answer Discuss in Forum

   Consider top portion
   
   

   σ1 =	250 × 103	= 25 MPa
   	100 × 100

   
   Consider bottom portion
   

   σ2 =	50 × 103	= 20 MPa
   	50 × 50

   
   ∴ σ_max = σ₂ = 25 MPa

   Correct Option: C

   Consider top portion
   
   

   σ1 =	250 × 103	= 25 MPa
   	100 × 100

   
   Consider bottom portion
   

   σ2 =	50 × 103	= 20 MPa
   	50 × 50

   
   ∴ σ_max = σ₂ = 25 MPa

---

---

48. The stiffness K of a beam deflecting in a symmetric mode, as shown in the figure, is
    

1. 1. 	EI
      	L

   
   
   

   2. 	2EI
      	L

   
   
   

   3. 	4EI
      	L

   
   
   

   4. 	6EI
      	L

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

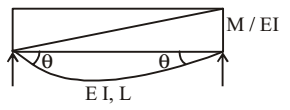
   θ =	ML
   	2EI

   
   

   ∴ M =	2EI	.θ
   	L

   
   

   θ = 1 ⇒ M =	2EI
   	L

   
   Which is the stiffness of the beam.

   Correct Option: B

   
   

   θ =	ML
   	2EI

   
   

   ∴ M =	2EI	.θ
   	L

   
   

   θ = 1 ⇒ M =	2EI
   	L

   
   Which is the stiffness of the beam.

---

49. A long structural column (length = L) with both ends hinged is acted upon by an axial compressive load, P. The differential equation governing the bending of column is given by
    

    EI	d2y	= - py
    	dx2

    
    Where y is the structural lateral deflection and EI is the flexural rigidity. The first critical load on column responsible for its buckling is given by

1. 1. 	π2EI
      	L2

   
   
   

   2. 	√2π2EI
      	L2

   
   
   

   3. 	2π2EI
      	L2

   
   
   

   4. 	4π2EI
      	L2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Effective length, L = l
   

   Critical load, Pc =	π2	EI
   	L2

   Correct Option: A

   Effective length, L = l
   

   Critical load, Pc =	π2	EI
   	L2

---

---

50. In a redundant joint model, three bar members are pin connected at Q as shown in the figure. Under some load placed at Q, the elongation of the members MQ and OQ are found to be 48 mm and 35 mm respectively. Then the horizontal displacement u and the vertical displacement v of the node Q, in mm, will be respectively.
    

1. 1. –6. 64 and 56.14

   
   
   

   2. 6.64 and 56.14

   
   
   

   3. 0.0 and 59.41

   
   
   

   4. 59.41 and 0.0

   
   
   

---

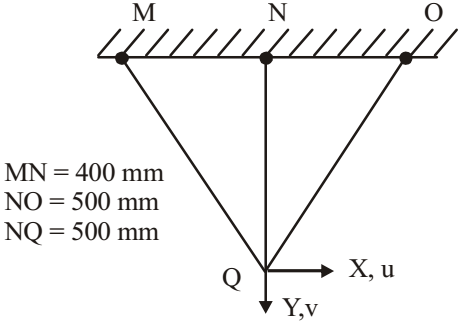
1. View Hint View Answer Discuss in Forum

   tanθ1 =	400	= 0.8
   	500

   
   ∴ θ₁ = 38.66°
   
   

   tanθ2 =	500	= 1
   	500

   
   ∴ θ₂ = 45°
   Along MQ,
   u sin 38.66° + v cos 38.66° = 48
   Along OQ
   –u sin 45° + v cos 45° = 35
   Solving, for u and v, we get
   u = 6.64 mm, v = 56.14 mm

   Correct Option: B

   tanθ1 =	400	= 0.8
   	500

   
   ∴ θ₁ = 38.66°
   
   

   tanθ2 =	500	= 1
   	500

   
   ∴ θ₂ = 45°
   Along MQ,
   u sin 38.66° + v cos 38.66° = 48
   Along OQ
   –u sin 45° + v cos 45° = 35
   Solving, for u and v, we get
   u = 6.64 mm, v = 56.14 mm

---