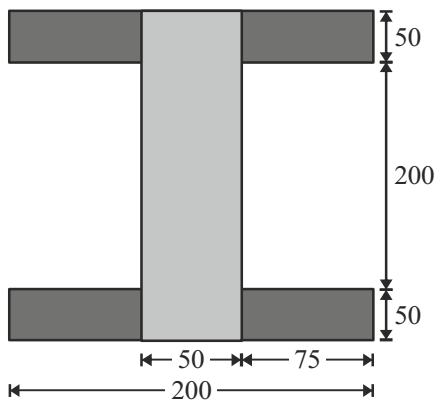
156. T-section of a beam is formed by gluing wooden planks as shown in the figure below. If this beam transmits a constant vertical shear force of 3000 K, the glue at any of the four joints will be subjected to a shear force (in kN per metre length) of
     

1. 1. 3.0

   
   
   

   2. 4.0

   
   
   

   3. 8.0

   
   
   

   4. 10.7

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Shear flow, q =	Vθ
   	I

   
   

   I =	50 × (300)3	+ 2		150 × 503	+ 15 × 50 + 1252
   	12			12

   
   = 3.5 × 10⁸ mm⁴
   V = 3000 N
   θ = 50 ×75 × 125 = 468750 mm²
   

   ∴ q =	3000 × 468750	= 4 kN/m
   	3.5 × 108

   Correct Option: B

   Shear flow, q =	Vθ
   	I

   
   

   I =	50 × (300)3	+ 2		150 × 503	+ 15 × 50 + 1252
   	12			12

   
   = 3.5 × 10⁸ mm⁴
   V = 3000 N
   θ = 50 ×75 × 125 = 468750 mm²
   

   ∴ q =	3000 × 468750	= 4 kN/m
   	3.5 × 108

---

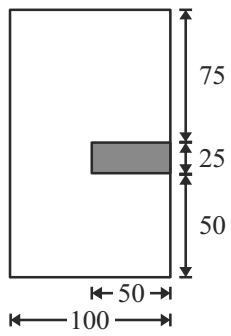
157. A beam with the cross-section given below is subjected to a positive bending moment (causing compression at the top) of 16 kN^–m acting around the horizontal axis. The tensile
     

1. 1. zero

   
   
   

   2. 5.9 kN

   
   
   

   3. 8.9 kN

   
   
   

   4. 17.8 kN

   
   
   

---

1. View Hint View Answer Discuss in Forum

   	M	=	f	=	E
   	I		y		R

   
   

   f =	m.y
   	I

   
   

   f(at 25 mm) =	m	× 25
   	I

   
   

   =	16 × 106	× 25
   	(1/12) × 100 × 1503

   
   = 14.22 N/mm²
   Force in shaded area
   = (1/2) × 14.22 × (area of shaded portion)
   = (1/2) × 14.22 × 25 × 50 = 8.9kN

   Correct Option: C

   	M	=	f	=	E
   	I		y		R

   
   

   f =	m.y
   	I

   
   

   f(at 25 mm) =	m	× 25
   	I

   
   

   =	16 × 106	× 25
   	(1/12) × 100 × 1503

   
   = 14.22 N/mm²
   Force in shaded area
   = (1/2) × 14.22 × (area of shaded portion)
   = (1/2) × 14.22 × 25 × 50 = 8.9kN

---

---

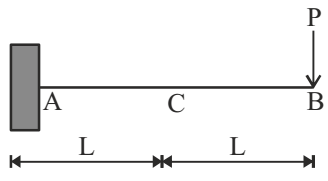
158. Consider the beam AB shown in the figure below. Part AC of the beam is rigid while part CB has the flexural rigidity EI. Identify the correct combination of deflection at end B and bending moment.
     

1. 1. 	PL3	, 2PL
      	3EI

   
   
   

   2. 	PL3	, PL
      	3EI

   
   
   

   3. 	8PL3	, 2PL
      	3EI

   
   
   

   4. 	8PL3	, PL
      	3EI

   
   
   

---

1. View Hint View Answer Discuss in Forum

   δB =	PL3
   	3EI

   
   MI at A = 2PL

   Correct Option: A

   δB =	PL3
   	3EI

   
   MI at A = 2PL

---

159. For the section shown below, second moment of the area about an axis d/4 distance above the bottom of the area is
     

1. 1. 	bd3
      	48

   
   
   

   2. 	bd3
      	12

   
   
   

   3. 	7bd3
      	48

   
   
   

   4. 	bd3
      	3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   MI about neutral axis
   

   =	1	bd3
   	12

   
   Seund MI = I_ca + Ax^-2
   (parallel axis theorem)
   

   =	1	bd3 + bd ×		d		2
   	12			4

   
   

   2b

   b2 + ω2

   Correct Option: C

   MI about neutral axis
   

   =	1	bd3
   	12

   
   Seund MI = I_ca + Ax^-2
   (parallel axis theorem)
   

   =	1	bd3 + bd ×		d		2
   	12			4

   
   

   2b

   b2 + ω2

---

---

160. A long shaft of diameter d is subjected to twisting moment T at its ends. The maximum normal stress acting at its cross-section is equal to

1. 1. zero

   
   
   

   2. 	16T
      	πd3

   
   
   

   3. 	32T
      	πd3

   
   
   

   4. 	64T
      	πd3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   J =	π	d4
   	32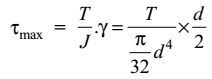

   
   
   

   2b

   b2 + ω2

   
   

   σn =	(σ1 + σ2)	+	(σ1 - σ2)	cos2θ = τsin2θ
   	2		2

   
   σ₁ = 0, σ₂ = 0, θ = 45°
   

   σn(max) = 0 + 0 - τmax × 1 =	16T
   	πd3

   Correct Option: B

   J =	π	d4
   	32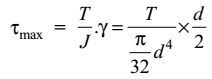

   
   
   

   2b

   b2 + ω2

   
   

   σn =	(σ1 + σ2)	+	(σ1 - σ2)	cos2θ = τsin2θ
   	2		2

   
   σ₁ = 0, σ₂ = 0, θ = 45°
   

   σn(max) = 0 + 0 - τmax × 1 =	16T
   	πd3

---