81. Polar moment of inertia (I_p), in cm4, of a rectangular section having width, b = 2 cm and depth, d = 6 cm is _________

1. 1. 40

   
   
   

   2. 34

   
   
   

   3. 33

   
   
   

   4. 46

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Polar MI, I_p = I_x + I_y
   

   =	bd3	+	bd3	=	bd	(d2 + b2)
   	12		12		12

   
   

   =	2 × 6	(62 + 22)
   	12

   
   = 1 × (36 + 4) = 40 cm⁴.

   Correct Option: A

   Polar MI, I_p = I_x + I_y
   

   =	bd3	+	bd3	=	bd	(d2 + b2)
   	12		12		12

   
   

   =	2 × 6	(62 + 22)
   	12

   
   = 1 × (36 + 4) = 40 cm⁴.

---

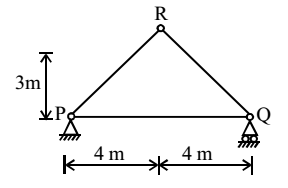
82. For the truss shown below, the member PQ is sort by 3 mm. The magnitude of vertical displacement of joint R (in mm) is ___________.
    

1. 1. 1 to 2.5

   
   
   

   2. 1 to 3.5

   
   
   

   3. 1 to 4.5

   
   
   

   4. 1 to 5.5

   
   
   

---

1. View Hint View Answer Discuss in Forum

   PQ is short by 3 mm.
   Apply unit load at R upwards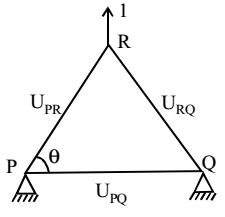
   
   U_PR × sin θ = 1/2
   U_PQ + U_PR cos θ = 0
   

   UPQ = - UPR cos θ = -	l	cos θ
   	2sin θ

   
   

   = -	l	cos θ
   	2

   
   

   =	- 1	×	4
   	2		3

   
   = - 2/3
   ∆R = U_PQ × λ_PQ
   

   =	- 2	(- 3)
   	3

   
   = 2 mm upwards

   Correct Option: A

   PQ is short by 3 mm.
   Apply unit load at R upwards
   
   U_PR × sin θ = 1/2
   U_PQ + U_PR cos θ = 0
   

   UPQ = - UPR cos θ = -	l	cos θ
   	2sin θ

   
   

   = -	l	cos θ
   	2

   
   

   =	- 1	×	4
   	2		3

   
   = - 2/3
   ∆R = U_PQ × λ_PQ
   

   =	- 2	(- 3)
   	3

   
   = 2 mm upwards

---

---

83. For the cantilever beam of span 3 m (shown below), a concentrated load of 20 kN applied at the free end causes a vertical displacement of 2 mm at a section located at a distance of 1m from the fixed end. If a concentrated vertically downward load of 10 kN is applied at the section located at a distance of 1 m from the fixed end (with no other load on the beam), the maximum vertical displacement in the same beam (in mm) is __________.
    

1. 1. 3

   
   
   

   2. 4

   
   
   

   3. 2

   
   
   

   4. 1

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
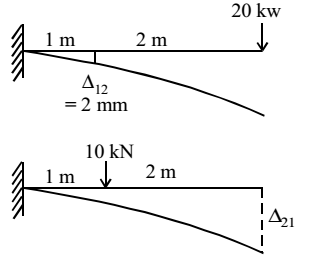
   From beam q is law,
   P1 × ∆₁₂ = P₂ × ∆₂₁
   10 × 2 = 20 × ∆₂₁
   ∴ ∆₂₁ = 1 mm

   Correct Option: D

   
   From beam q is law,
   P1 × ∆₁₂ = P₂ × ∆₂₁
   10 × 2 = 20 × ∆₂₁
   ∴ ∆₂₁ = 1 mm

---

84. If the magnitude of load P is increased till collapse and the plastic moment carrying capacity of steel beam section is 90 kNm, determine reaction R(in kN) (correct to 1-decimal place) using plastic analysis.

1. 1. 60

   
   
   

   2. 33

   
   
   

   3. 55

   
   
   

   4. 44

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

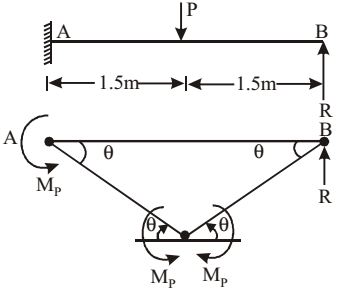
   - MPθ + P	l	θ =0
   	2

   
   

   ∴ Pu =	MP	=	6 × 90	= 180 kN
   	l		3

   
   At collapse condition SM_A = 0
   R × 3 + M_P – P × 1.5 – M_P + M_P = 0
   ⇒ R = 60 kN

   Correct Option: A

   
   

   - MPθ + P	l	θ =0
   	2

   
   

   ∴ Pu =	MP	=	6 × 90	= 180 kN
   	l		3

   
   At collapse condition SM_A = 0
   R × 3 + M_P – P × 1.5 – M_P + M_P = 0
   ⇒ R = 60 kN

---

---

85. If load P = 80 kN, find the reaction R(in kN) (correct to 1-decimal place) using elastic analysis.

1. 1. 25

   
   
   

   2. 33

   
   
   

   3. 22

   
   
   

   4. 33

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Equating deflection at end R
   Let l = 3 m
   

   ∴	R(l)3	=	P(1.5)3	+	P(1.5)2	× 1.5
   	3EI		3EI		2EI

   
   
   

   ⇒	R(3)3	=	1.125P	+	1.6875P
   	3EI		EI		EI

   
   

   	9R	=	1.125P	+	1.6875P
   	EI		EI		EI

   
   

   ⇒ R =	5	P
   	16

   
   

   or R =	5	× 80 = 25 kN
   	16

   Correct Option: A

   Equating deflection at end R
   Let l = 3 m
   

   ∴	R(l)3	=	P(1.5)3	+	P(1.5)2	× 1.5
   	3EI		3EI		2EI

   
   
   

   ⇒	R(3)3	=	1.125P	+	1.6875P
   	3EI		EI		EI

   
   

   	9R	=	1.125P	+	1.6875P
   	EI		EI		EI

   
   

   ⇒ R =	5	P
   	16

   
   

   or R =	5	× 80 = 25 kN
   	16

---