166. For the linear elastic beam shown in the figure, the flexural rigidity. EI, is 781250 kN-m². When w = 10 kN/m, the
     vertical reaction R_A at A is 50 kN. The value of R_A for w = 100 kN/m is
     

1. 1. 500 kN

   
   
   

   2. 425 kN

   
   
   

   3. 250 kN

   
   
   

   4. 75 kN

   
   
   

---

1. View Hint View Answer Discuss in Forum

   10 kN/ m load
   

   Deflection, δ =	wl4
   	8EI

   
   

   =	10 × 54	= 1 mm < 6 mm
   	8 × 781250

   
   ∴ There is no reaction at B.
   100 kN/m load
   

   Deflection, δ =	wl4	= 10 mm > 6 mm
   	8EI

   
   Reaction at B = deflection prevented at B
   = 10 – 6 = 4 mm.
   

   	RBl3	= 4 mm
   	3EI

   
   

   	RB × 53	= 4
   	3 × 781250

   
   ∴ R_B = 425 kN
   This is the value of R_A.

   Correct Option: B

   10 kN/ m load
   

   Deflection, δ =	wl4
   	8EI

   
   

   =	10 × 54	= 1 mm < 6 mm
   	8 × 781250

   
   ∴ There is no reaction at B.
   100 kN/m load
   

   Deflection, δ =	wl4	= 10 mm > 6 mm
   	8EI

   
   Reaction at B = deflection prevented at B
   = 10 – 6 = 4 mm.
   

   	RBl3	= 4 mm
   	3EI

   
   

   	RB × 53	= 4
   	3 × 781250

   
   ∴ R_B = 425 kN
   This is the value of R_A.

---

167. A homogeneous simply supported prismatic beam of width B, depth D and span L is subjected to a concentrated load of magnitude P. The load can be placed anywhere along the span of the beam. The maximum flexural stress developed in beam is

1. 1. 	2		PL
      	3		BD2

   
   
   

   2. 	3		PL
      	4		BD2

   
   
   

   3. 	4		PL
      	3		BD2

   
   
   

   4. 	3		PL
      	2		BD2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   f =	m
   	z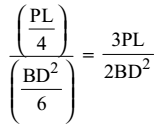

   
   

   Correct Option: D

   f =	m
   	z

   
   

---

---

168. For the plane frame with an overhang as shown below, assuming negligible axial deformation, the degree of static indeterminacy, d, and the degree of kinematic indeterminacy, k, are
     

1. 1. d = 3 and k = 10

   
   
   

   2. d = 3 and k = 13

   
   
   

   3. d = 9 and k = 10

   
   
   

   4. d = 9 and k = 13

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Degree of static indeterminary (d)
   Total unknown reactions = 3 + 3 + 2 + 1 = 9.
   Degree of kinematic indeterminary =(3j – r) – m
   = [3 × 10 – (3 + 2 + 1)] – 11 = 13

   Correct Option: D

   Degree of static indeterminary (d)
   Total unknown reactions = 3 + 3 + 2 + 1 = 9.
   Degree of kinematic indeterminary =(3j – r) – m
   = [3 × 10 – (3 + 2 + 1)] – 11 = 13

---

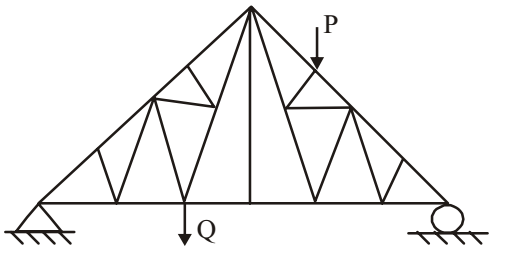
169. For the plane truss shown in the figure, the number of zero force members for the given loading is
     

1. 1. 4

   
   
   

   2. 8

   
   
   

   3. 11

   
   
   

   4. 13

   
   
   

---

1. View Hint View Answer Discuss in Forum

   If at any joint or junction, there are three forces acting and out of those two are in same line, then the third force is zero.
   

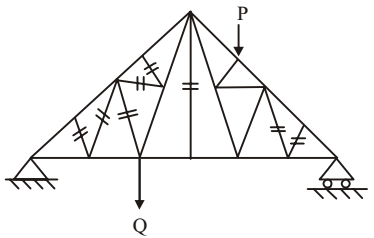
   Correct Option: B

   If at any joint or junction, there are three forces acting and out of those two are in same line, then the third force is zero.
   

---

---