106. For the plane stress situation shown in the figure, the maximum shear stress and the plane on which it acts are:
     

1. 1. – 50 MPa, on a plane 45° clockwise w.r.t. x-axis

   
   
   

   2. – 50 MPa, on a plane 45° anti-clockwise w.r.t. x-axis

   
   
   

   3. 50 MPa, at all orientations

   
   
   

   4. Zero, at all orientations

   
   
   

---

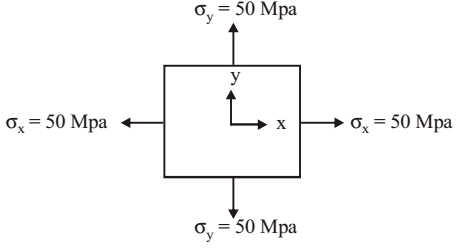
1. View Hint View Answer Discuss in Forum

   τθ =	σx - σy	= sin2θ + τxycos2θ
   	z

   
   τ_xy = 0
   σ_x and σ_y are equal.
   ∴ τ_θ = 0 + 0 = 0 (in all direction orientations)

   Correct Option: D

   τθ =	σx - σy	= sin2θ + τxycos2θ
   	z

   
   τ_xy = 0
   σ_x and σ_y are equal.
   ∴ τ_θ = 0 + 0 = 0 (in all direction orientations)

---

107. A guided support as shown in the figure below is represented by three springs (horizontal, vertical and rotational) with stiffness k_x, k_y and kq respectively. The limiting values of k_x, k_y and k_θ are:
     

1. 1. ∞, 0, ∞

   
   
   

   2. ∞, ∞, ∞

   
   
   

   3. 0, ∞, ∞

   
   
   

   4. ∞, ∞, 0

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Stiffness = Force/Deflection
   As per given figure rotation and horizontal deflection is zero
   ∴ Stiffness is ∞. Stiffness is zero in y direction.

   Correct Option: A

   Stiffness = Force/Deflection
   As per given figure rotation and horizontal deflection is zero
   ∴ Stiffness is ∞. Stiffness is zero in y direction.

---

---

108. For the beam shown below, the stiffness coefficient K₂₂ can be written as
     

1. 1. 	6EI
      	L2

   
   
   

   2. 	12EI
      	L3

   
   
   

   3. 	3EI
      	L

   
   
   

   4. 	EI
      	6L2

   
   
   

---

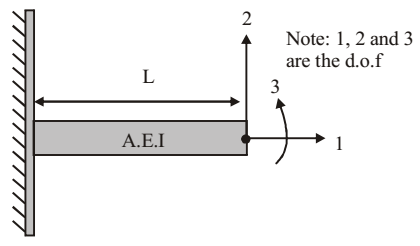
1. View Hint View Answer Discuss in Forum

   
   

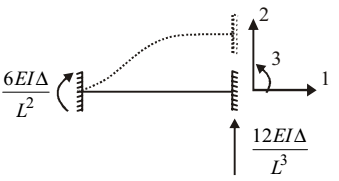
   K22 =	12 EI
   	L3

   Correct Option: B

   
   

   K22 =	12 EI
   	L3

---

109. The tension (in kN) in a 10 m long cable, shown in the figure, neglecting its self-weight is]
     

1. 1. 120

   
   
   

   2. 75

   
   
   

   3. 60

   
   
   

   4. 45

   
   
   

---

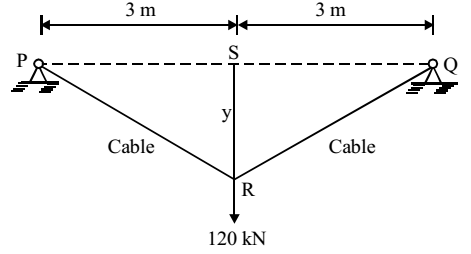
1. View Hint View Answer Discuss in Forum

   
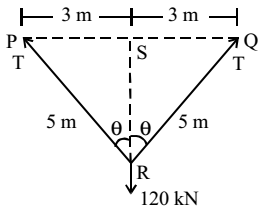
   S F_y = 0
   ⇒ 2T cos θ = 120
   From fig. SR = 4 m
   ∴ cos θ = 4/5
   2T × 4/5 = 120
   ∴ T = 75 kN

   Correct Option: B

   
   S F_y = 0
   ⇒ 2T cos θ = 120
   From fig. SR = 4 m
   ∴ cos θ = 4/5
   2T × 4/5 = 120
   ∴ T = 75 kN

---

---

110. A prismatic beam (as shown below) has plastic moment capacity of Mp, then the collapse load P of the beam is
     

1. 1. 	2MP
      	L

   
   
   

   2. 	4MP
      	L

   
   
   

   3. 	6MP
      	L

   
   
   

   4. 	8MP
      	L

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Degree of static indeterminacy, D_s = 0
   For mechanical, no. of plastic hinges required = D_s + 1 = 1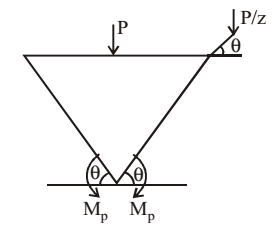
   
   From principle of virtual work
   

   - MP θ - MP θ + P.	L	θ -	P	×	L	θ = 0
   	2		2		3

   
   

   - MP θ +	PL	θ -	PL	θ = 0
   	2		6

   
   

   2MP =	PL	×	PL
   	2		6

   
   

   =	(3 - 1)PL
   	6

   
   

   ⇒ 2MP =	1	PL
   	3

   
   

   ∴ P =	6MP
   	L

   Correct Option: C

   Degree of static indeterminacy, D_s = 0
   For mechanical, no. of plastic hinges required = D_s + 1 = 1
   
   From principle of virtual work
   

   - MP θ - MP θ + P.	L	θ -	P	×	L	θ = 0
   	2		2		3

   
   

   - MP θ +	PL	θ -	PL	θ = 0
   	2		6

   
   

   2MP =	PL	×	PL
   	2		6

   
   

   =	(3 - 1)PL
   	6

   
   

   ⇒ 2MP =	1	PL
   	3

   
   

   ∴ P =	6MP
   	L

---