Engineering Mathematics Miscellaneous Easy Questions and Answers | Page - 29

Engineering Mathematics Miscellaneous

The variable x takes a value between 0 and 10 with uniform probability distribution. The variable y takes a value between 0 and 20 with uniform probability distribution. The probability of the sum of variables (x + y) being greater than 20 is

1. 0.33
1. 0.25
1. 0
1. 0.50

View Hint View Answer Discuss in Forum

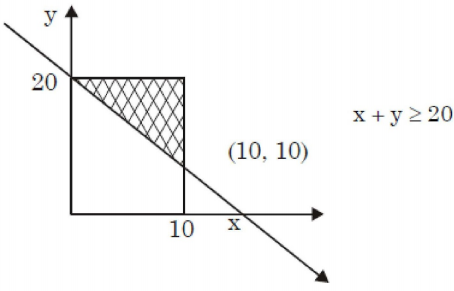
Required Probability (x + y > 20)
= Shaded Area
Total Area

= 1/2 × 10 × 10
20 × 10

= 50 = 0.25
200

Correct Option: B

Required Probability (x + y > 20)
= Shaded Area
Total Area

= 1/2 × 10 × 10
20 × 10

= 50 = 0.25
200

Three vendors were asked to supply a very high precision component. The respective probabilities of their meeting the strict design specifications are 0.8, 0.7 and 0.5. Each vendor supplies one component. The probability that out of total three components supplied by the vendors, at least one will meet the design specification is ______.

1. 0.97
1. 0.99
1. 0.92
1. 0.91

View Hint View Answer Discuss in Forum

Probability (at least one will meet specification)
= 1 – probability (none will meet specification)
= 1 – (1 – 0.8) × (1 – 0.7) × (1 – 0.5)
= 1 – 0.2 × 0.3 × 0.5 = 1 – 0.03 = 0.97

Correct Option: A

Probability (at least one will meet specification)
= 1 – probability (none will meet specification)
= 1 – (1 – 0.8) × (1 – 0.7) × (1 – 0.5)
= 1 – 0.2 × 0.3 × 0.5 = 1 – 0.03 = 0.97

Let z be a complex variable. For a counterclockwise integration around a unit circle C, centred at origin.
∮_c 1 dz = Aπ i the value of A is
5z - 4

1. 2/5
1. 1/2
1. 2
1. 4/5

View Hint View Answer Discuss in Forum

∮_c 1 dz = Aπi
5z - 4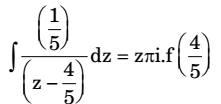

2 πi
5

A = 2 = 0.4
5

Correct Option: A

∮_c 1 dz = Aπi
5z - 4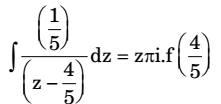

2 πi
5

A = 2 = 0.4
5

F(z) is a function of the complex variable z = x + iy given by
F(z) = iz + k Re(z) + i Im(z)
For what value of k will F(z) satisfy the Cauchy Riemann equations?

1. 0
1. 1
1. –1
1. y

View Hint View Answer Discuss in Forum

By Cauchy -Riemann equations
u_x = v_y
u + iv = i (x + iy) + kx + iy
u + iv = kx – y + i (x + y)
u = kx – y, v = x + y
u_x = k, u_y = –1
v = x + y
v_x = 1; v_y = 1
u_x = v_y
k = 1

Correct Option: B

By Cauchy -Riemann equations
u_x = v_y
u + iv = i (x + iy) + kx + iy
u + iv = kx – y + i (x + y)
u = kx – y, v = x + y
u_x = k, u_y = –1
v = x + y
v_x = 1; v_y = 1
u_x = v_y
k = 1

If f(z) = (x² + ay²) + ibxy is a complex analytic function of z = x + iy, where i = √- 1, then

1. a = –1, b = –1
1. a= –1, b = 2
1. a = 1, b = 2
1. a = 2, b = 2

View Hint View Answer Discuss in Forum

For analytic function,
f (2) = (x² + a y²) + ibxy
u + iv = (x² + ay²) + i (bxy)
u = x² + ay²; v = bxy
u_x = 2x; u_y = 2 ay
V_x = b_y; V_y = bx
u_x = V_y; u_y = –V_x
2 x = bx; 2ay = –by
By solving, we get
a = –1 b = 2

Correct Option: B

For analytic function,
f (2) = (x² + a y²) + ibxy
u + iv = (x² + ay²) + i (bxy)
u = x² + ay²; v = bxy
u_x = 2x; u_y = 2 ay
V_x = b_y; V_y = bx
u_x = V_y; u_y = –V_x
2 x = bx; 2ay = –by
By solving, we get
a = –1 b = 2