Engineering Mathematics Miscellaneous
- The divergence of the vector field (x - y)î + (y - x)ĵ + (x + y + z)k̂ is
-
View Hint View Answer Discuss in Forum
∇ . A = δ(x - y) + δ(y - x) + δ (x + y + z) δx δy δz
= 1 + 1 + 1 = 3Correct Option: D
∇ . A = δ(x - y) + δ(y - x) + δ (x + y + z) δx δy δz
= 1 + 1 + 1 = 3
- The area of a triangle formed by the tips of vectors a,b and c is
-
View Hint View Answer Discuss in Forum
Let the vectors be
i, j, i + j
(c) (b) (a)
Now Area vector will be perpendicular to place of x, y i.e. z k will be the required unit vector Now, (a), (d) con not give vector product
Correct Option: B
Let the vectors be
i, j, i + j
(c) (b) (a)
Now Area vector will be perpendicular to place of x, y i.e. z k will be the required unit vector Now, (a), (d) con not give vector product
- The line integral ∫V . dr of the vector V(r)
= 2xyzî + x2zî + x2ĵ + xyk̂ from the origin to the point P(1, 1, 1)
-
View Hint View Answer Discuss in Forum
Since, potential function of V is x2yz
∴ (x2yz) at (1, 1, 1) — x2yz at (0, 0, 0) = 1Correct Option: A
Since, potential function of V is x2yz
∴ (x2yz) at (1, 1, 1) — x2yz at (0, 0, 0) = 1
- Stokes theorem connects
-
View Hint View Answer Discuss in Forum
Stokes theorem connects a line integral and a surface integral.
Correct Option: A
Stokes theorem connects a line integral and a surface integral.
- In matrix equation [A]{X} = {R},

One of the eigenvalues of matrix [A] is
-
View Hint View Answer Discuss in Forum
In matrix equation
A[X] = {R} A[X] can also be substituted by λ[X]
Choosing from option ‘16’ first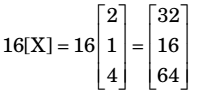
As 16 satisfies the equation, the correct option is (a).Correct Option: A
In matrix equation
A[X] = {R} A[X] can also be substituted by λ[X]
Choosing from option ‘16’ first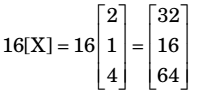
As 16 satisfies the equation, the correct option is (a).

