121. Which one of the following equations is a correct identity for arbitrary 3 × 3 real matrices P, Q and R?

1. 1. P(Q + R) = PQ + RP

   
   
   

   2. (P – Q)² = P² – 2PQ + Q²

   
   
   

   3. det (P + Q) = detP + detQ

   
   
   

   4. (P + Q)² = P² + PQ + QP + Q²

   
   
   

---

1. View Hint View Answer Discuss in Forum

   This is a standard relation.
   (P + Q)² = P² + PQ + QP + Q²

   Correct Option: D

   This is a standard relation.
   (P + Q)² = P² + PQ + QP + Q²

---

122. For a matrix [M] =
     
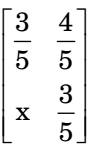
     , the transpose of the matrix is equal to the inverse of the matrix,[M]T = [M]–1. The value of x is given by

1. 1. -	4
      	5

   
   
   

   2. -	3
      	5

   
   
   

   3. 	3
      	5

   
   
   

   4. 	4
      	5

      
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   A^T = A^-1
   so, orthogonal matrix
   Now AA^-1 = I = AA^T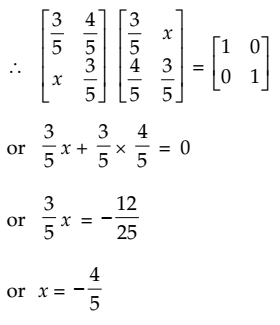
   
   

   Correct Option: A

   A^T = A^-1
   so, orthogonal matrix
   Now AA^-1 = I = AA^T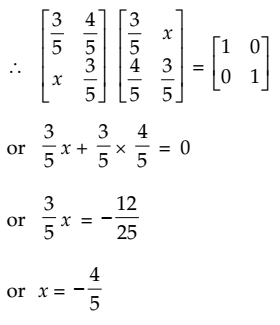
   
   

---

---

123. Multiplication of matrices E and F is G. Matrices E and G are
     

1. 1. 

   
   
   

   2. 

   
   
   

   3. 

   
   
   

   4. 

   
   
   

---

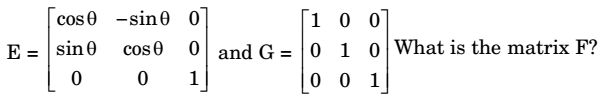
1. View Hint View Answer Discuss in Forum

   
   We know that product of (E × F) is unit matrix 50 F will be the inverse of E.
   Now E × F = G
   ∴ F = E^-1

   Correct Option: C

   
   We know that product of (E × F) is unit matrix 50 F will be the inverse of E.
   Now E × F = G
   ∴ F = E^-1

---

124. Match the items in columns I and II
     Column I
     P. Singular matrix
     Q. Non-square matrix
     R. Real symmetric
     S. Orthogonal matrix
     Column II
     1. Determinant is not defined
     2. Determinant is always one
     3. Determinant is zero
     4. Eigenvalues are always real
     5. Eigenvalues are not defined

1. 1. P–3, Q–1, R–4, S–2

   
   
   

   2. P–2, Q–3, R–4, S–1

   
   
   

   3. P–3, Q–2, R–5, S–4

   
   
   

   4. P–3, Q–4, R–2, S–1

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: A

   NA

---

---

125. The Fourier cosine series for an even function f(x) is given by
     
     The value of the coefficient a₂ for the function f(x) = cos²(x) in [0, π] is

1. 1. –0.5

   
   
   

   2. 0.0

   
   
   

   3. 0.5

   
   
   

   4. 1.0

   
   
   

---

1. View Hint View Answer Discuss in Forum

   cos2x =	1 + cos2x
   	2

   
   

   f(x) =	1	+	cos2x
   	2		2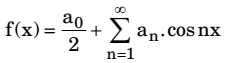

   
   
   a₀ = 1
   a₁ = 0
   a₂ = 1/2

   Correct Option: C

   cos2x =	1 + cos2x
   	2

   
   

   f(x) =	1	+	cos2x
   	2		2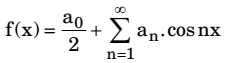

   
   
   a₀ = 1
   a₁ = 0
   a₂ = 1/2

---