186. For the matrix A =		5		3		,
     		1		3

     
     ONE of the normalized eigen vectors is given as

1. 1. 

   
   
   

   2. 

   
   
   

   3. 

   
   
   

   4. 

   
   
   

---

1. View Hint View Answer Discuss in Forum

   | A - λI | = 0
   
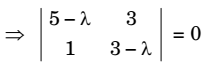
   ⇒ (5 – λ) (3 – λ) = 3 = 0
   ⇒ λ² – 8λ + 15 – 3 = 0
   ⇒ λ² – 8λ + 12 = 0
   ⇒ λ = 2, λ = 6
   Now, at λ = 2, eign vector:
   
   Hence required vector is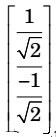
   

   Correct Option: B

   | A - λI | = 0
   
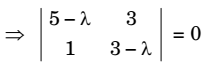
   ⇒ (5 – λ) (3 – λ) = 3 = 0
   ⇒ λ² – 8λ + 15 – 3 = 0
   ⇒ λ² – 8λ + 12 = 0
   ⇒ λ = 2, λ = 6
   Now, at λ = 2, eign vector:
   
   Hence required vector is
   

---

187. Laplace transform of the function f(t) is given by F(s) = L{f(t)} =

     
     Laplace transform of the function shown below is given by
     
     

1. 1. 1 - e-2s

      s

      
      

   
   
   

   2. 1 - e-s

      2s

      
      

   
   
   

   3. 2 - 2e-s

      s

      
      

   
   
   

   4. 1 - 2e-s

      s

   
   
   

---

1. View Hint View Answer Discuss in Forum

   f(t) = 2; 0 < t < 1 > 0; otherwise
   

   ∴ L[f(t)] =

   
   

   =	2 - 2e-s
   	s

   Correct Option: C

   f(t) = 2; 0 < t < 1 > 0; otherwise
   

   ∴ L[f(t)] =

   
   

   =	2 - 2e-s
   	s

---

---

188. The Laplace transform of e^i5t where i = √-1, is
     

1. 1. s - 5i

      s2 - 25

      
      

   
   
   

   2. s + 5i

      s2 + 25

      
      

   
   
   

   3. s + 5i

      s2 - 25

      
      

   
   
   

   4. s - 5i

      s2 + 25

   
   
   

---

1. View Hint View Answer Discuss in Forum

   ∴ L[ei5t] =	1
   	s + 5i

   
   

   =	1	×	(s + 5i)
   	(s - 5i)		(s + 5i)

   
   

   =	s + 5i
   	s2 + 25

   
   

   Correct Option: B

   ∴ L[ei5t] =	1
   	s + 5i

   
   

   =	1	×	(s + 5i)
   	(s - 5i)		(s + 5i)

   
   

   =	s + 5i
   	s2 + 25

   
   

---

189. Laplace transform of cos(ωt) is	s
     	s2 + ω2

     
     The laplace transform of e^–2t cos(4t) is
     

1. 1. s - 2

      (s - 2)2 + 16

      
      

   
   
   

   2. s + 2

      (s - 2)2 + 16

      
      

   
   
   

   3. s - 2

      (s + 2)2 + 16

      
      

   
   
   

   4. s + 2

      (s + 2)2 + 16

   
   
   

---

1. View Hint View Answer Discuss in Forum

   We know that if L{f(t)} = F(s)
   Then L{e^at f(t)} = F(s – a)
   

   ∴ L[e-2t cos 4t ] =	s + 2
   	(s + 2)2 + 42

   
   

   =	s + 2
   	(s + 2)2 + 16

   Correct Option: D

   We know that if L{f(t)} = F(s)
   Then L{e^at f(t)} = F(s – a)
   

   ∴ L[e-2t cos 4t ] =	s + 2
   	(s + 2)2 + 42

   
   

   =	s + 2
   	(s + 2)2 + 16

---

---

190. Laplace transform of cos (ωt) is
     

1. 1. s

      s2 + ω2

      
      

   
   
   

   2. ω

      s2 + ω2

      
      

   
   
   

   3. s

      s2 - ω2

      
      

   
   
   

   4. ω

      s2 - ω2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Laplace transform of cos (ωt) is
   

   L[ cos (ωt) ] =	S
   	s2 + ω2

   Correct Option: A

   Laplace transform of cos (ωt) is
   

   L[ cos (ωt) ] =	S
   	s2 + ω2

---