C = [A: B]_{3 × 5}
∴ ρ [C_{3 × 5} ] <e; min [3,5}
Since the system is inconsistent
ρ(A) < ρ(C)
∴ ρ (A) < 3
Hence, the maximum possible rank of A = 2

Correct Option: C

C = [A: B]_{3 × 5}
∴ ρ [C_{3 × 5} ] <e; min [3,5}
Since the system is inconsistent
ρ(A) < ρ(C)
∴ ρ (A) < 3
Hence, the maximum possible rank of A = 2

Given equations are
x + 2y + z = 6
2x + y + 2z = 6
x + y + z = 5
Given system can be written as

Applying row operation
R₂ → R₂ – 2R₁, R₃ → R₃ – R₁

and applying R₃ → 3R₃ – R₁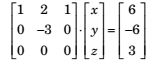

Since the rank of co-efficient matrix is 2 and rank of argument matrix is 3, which is not equal. Hence system has no solution.

Correct Option: C

Given equations are
x + 2y + z = 6
2x + y + 2z = 6
x + y + z = 5
Given system can be written as

Applying row operation
R₂ → R₂ – 2R₁, R₃ → R₃ – R₁

and applying R₃ → 3R₃ – R₁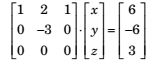

Since the rank of co-efficient matrix is 2 and rank of argument matrix is 3, which is not equal. Hence system has no solution.

|A| = 4
= 4

Correct Option: D

|A| = 4
= 4

The product of eigen value of any matrix is equal to the determinant value of the matrix λ₁ = 10 , λ₂ = unknown
|A| = 50
λ₁ .λ₂ = 50
10(λ₂) = 50
∴ λ₂ = 5

Correct Option: B

The product of eigen value of any matrix is equal to the determinant value of the matrix λ₁ = 10 , λ₂ = unknown
|A| = 50
λ₁ .λ₂ = 50
10(λ₂) = 50
∴ λ₂ = 5

Correct Option: A

P =		4 + 3i			-i
		i			4 - 3i

P-1 =		4 - 3i			-(-i)
		-i			4 + 3i
			| A |

=	1		4 - 3i			i
	24		-i			4 + 3i