Engineering Mathematics Miscellaneous

Engineering Mathematics Miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Engineering Mathematics

Engineering Mathematics Miscellaneous
  1. Assuming i = √-1 and t is a real number 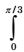eit dt is









  1. View Hint View Answer Discuss in Forum


    =
    1
    1
    		 +
    i√3
    		 - 1
    222

    =
    -1
    		 +
    √3
    		 =
    √3
    		 +
    i
    2i222

    Correct Option: A


    =
    1
    1
    		 +
    i√3
    		 - 1
    222

    =
    -1
    		 +
    √3
    		 =
    √3
    		 +
    i
    2i222

  1. Given that x¨ + 3x = 0 , and x(0) = 1, ẋ(0) what is x(1)?








  1. View Hint View Answer Discuss in Forum

    x¨ + 3x = 0
    ⇒ (D2 + 3)x = 0

    P.I. =
    1
    		(0) = 0
    D2 + 3

    Now C.F. is given by,
    C1em1t + C2em2t
    ∴ m2 + 3 = 0
    ⇒ m = ± i √3
    Hence the solution is C.F. + P.I.
    i.e. C1ei √3t + C2e-i √3t
    But x(0) = 1
    ⇒ C1 + C2 = 1
    and x(0) = 0, x = i √3 C1 ei √3t - i √3 C2 e-i √3t
    ⇒ x(0) = 0
    ⇒ C1 = C2 =
    1
    2

    ∴ x =
    1
    		[ ei √3t + e-i √3t ]
    2

    ⇒ x(1) =
    1
    		[ ei √3 + e(1 / i √3) ]
    2

    cos √3 = −0.16

    Correct Option: B

    x¨ + 3x = 0
    ⇒ (D2 + 3)x = 0

    P.I. =
    1
    		(0) = 0
    D2 + 3

    Now C.F. is given by,
    C1em1t + C2em2t
    ∴ m2 + 3 = 0
    ⇒ m = ± i √3
    Hence the solution is C.F. + P.I.
    i.e. C1ei √3t + C2e-i √3t
    But x(0) = 1
    ⇒ C1 + C2 = 1
    and x(0) = 0, x = i √3 C1 ei √3t - i √3 C2 e-i √3t
    ⇒ x(0) = 0
    ⇒ C1 = C2 =
    1
    2

    ∴ x =
    1
    		[ ei √3t + e-i √3t ]
    2

    ⇒ x(1) =
    1
    		[ ei √3 + e(1 / i √3) ]
    2

    cos √3 = −0.16

  1. For
    d2y
    		 + 4
    dy
    		 + 3y = 3e2x the particular integral is
    dx2dx









  1. View Hint View Answer Discuss in Forum

    The given differential equaiton may be written as
    D2y + 4Dy + 3y = 3e2x

    ∴ P.I. =
    3e2x
    (D2 + 4D + 3)

    Substituting D = 2, we get
    P.I. = 3e2x
    1
    		 =
    e2x
    155

    Correct Option: B

    The given differential equaiton may be written as
    D2y + 4Dy + 3y = 3e2x

    ∴ P.I. =
    3e2x
    (D2 + 4D + 3)

    Substituting D = 2, we get
    P.I. = 3e2x
    1
    		 =
    e2x
    155

Direction: The complete solution of the ordinary differential equation

d2y
 + p
dy
 + qy = 0 is
dx2dx

y = c1e-x + c2e-3x

  1. Which of the following is a solution of the differential equation
    d2y
    		 + p
    dy
    		 + (q + 1)y = 0 ?
    dx2dx









  1. View Hint View Answer Discuss in Forum

    d2y
    		 + p
    dy
    		 + (q + 1)y = 0
    dx2dx

    ∴ D2 + pD + (q + 1) = 0
    ⇒ D2 + 4D + 4 = 0
    Since, p = 4, q = 3, therefore
    ⇒ D =
    -4 ± √16 - 16
    		 = -2
    2

    Hence, it's solution is, = xeDx = xe–2x

    Correct Option: C

    d2y
    		 + p
    dy
    		 + (q + 1)y = 0
    dx2dx

    ∴ D2 + pD + (q + 1) = 0
    ⇒ D2 + 4D + 4 = 0
    Since, p = 4, q = 3, therefore
    ⇒ D =
    -4 ± √16 - 16
    		 = -2
    2

    Hence, it's solution is, = xeDx = xe–2x

  1. Then, p and q are








  1. View Hint View Answer Discuss in Forum

    d2y
    		 + p
    dy
    		 + qy = 0
    dx2dx

    D2 + pD + q = 0
    It's solutions is y = c1e-x + c2e-3x
    ⇒ m = –1, n = –3
    If m and n are two roots of the above equation, then
    m + n = –p,
    ⇒ –1 – 3 = –p,
    ⇒ p = 4
    and mn = q,
    ⇒ (–1) (–3) = q,
    ⇒ q = 3

    Correct Option: C

    d2y
    		 + p
    dy
    		 + qy = 0
    dx2dx

    D2 + pD + q = 0
    It's solutions is y = c1e-x + c2e-3x
    ⇒ m = –1, n = –3
    If m and n are two roots of the above equation, then
    m + n = –p,
    ⇒ –1 – 3 = –p,
    ⇒ p = 4
    and mn = q,
    ⇒ (–1) (–3) = q,
    ⇒ q = 3