91. The solution of the differential equation (dy / dx) + 2xy = e^-x² with y(0) = 1 is

1. 1. (1 + x) e^+x²

   
   
   

   2. (1 + x) e^-x²

   
   
   

   3. (1 - x) e^+x²

   
   
   

   4. (1 - x) e^-x²

   
   
   

---

1. View Hint View Answer Discuss in Forum

   First order equation,	dy	+ Py = Q, where P = 2x and Q = ex²
   	dx

   
   Since P and Q are functions of x, then
   ∴ Integrating factor,
   I.F. = e^+∫pdx = e^+x²
   

   ex²	dy	+ (2xex²)y = e-x² . e+x²
   	dx

   
   

   	d	(yex²) = 1
   	dx

   
   ye^x² = x + c
   Since, y(0) = 1, ⇒ C = 1
   ∴ y = (1 + x) e ^-x²

   Correct Option: B

   First order equation,	dy	+ Py = Q, where P = 2x and Q = ex²
   	dx

   
   Since P and Q are functions of x, then
   ∴ Integrating factor,
   I.F. = e^+∫pdx = e^+x²
   

   ex²	dy	+ (2xex²)y = e-x² . e+x²
   	dx

   
   

   	d	(yex²) = 1
   	dx

   
   ye^x² = x + c
   Since, y(0) = 1, ⇒ C = 1
   ∴ y = (1 + x) e ^-x²

---

92. If x²		dy	+ 2xy =	2ln(x)	, and y(1) = 0, then what is y(e)?
    		dx		x

1. 1. e

   
   
   

   2. 1

   
   
   

   3. 1/e

   
   
   

   4. 1/e²

   
   
   

---

1. View Hint View Answer Discuss in Forum

   x² y' + 2xy =	2 ln x
   	x

   
   

   ⇒ y' +	2	y =	2 ln x
   	x		x3

   
   

   Comparing, we get P =	2	Q =	2 ln x
   	x'		x3

   
   
   y(I.F.) = ∫ Q I.F. dx + c
   

   x² y = ∫	2 ln x	. x²dx + C
   	x3

   
   Solving above, find the value of C.
   Putting x = 1, then find the value of y at x = e.
   

   Which is y =	1
   	e2

   
   

   Correct Option: D

   x² y' + 2xy =	2 ln x
   	x

   
   

   ⇒ y' +	2	y =	2 ln x
   	x		x3

   
   

   Comparing, we get P =	2	Q =	2 ln x
   	x'		x3

   
   
   y(I.F.) = ∫ Q I.F. dx + c
   

   x² y = ∫	2 ln x	. x²dx + C
   	x3

   
   Solving above, find the value of C.
   Putting x = 1, then find the value of y at x = e.
   

   Which is y =	1
   	e2

   
   

---

---

93. The solution of the differential equation	dy	+ y = 0 is
    	dx

1. 1. y =	1
      	x + c

   
   
   

   2. y =	- x 3	+ c
      	3

   
   
   

   3. ce^x

   
   
   

   4. unsolvable as equation is non-linear

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given differential equation is
   

   	dy	+ y2 = 0
   	dx2

   
   

   ⇒	dy	-dx
   	y2

   
   On integration, we get
   

   ∫	dy	-∫ dx
   	y2

   
   

   -	1	= x - c
   	y

   
   where c is a constant
   

   ⇒ -	1	= -(x + c)
   	y

   
   

   ∴ y =	1
   	x + c

   
   

   Correct Option: A

   Given differential equation is
   

   	dy	+ y2 = 0
   	dx2

   
   

   ⇒	dy	-dx
   	y2

   
   On integration, we get
   

   ∫	dy	-∫ dx
   	y2

   
   

   -	1	= x - c
   	y

   
   where c is a constant
   

   ⇒ -	1	= -(x + c)
   	y

   
   

   ∴ y =	1
   	x + c

   
   

---

94. 

1. 1. 0

   
   
   

   2. 3

   
   
   

   3. 1

   
   
   

   4. - 1

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

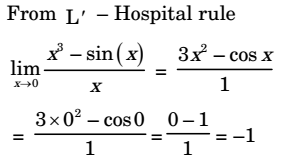
   Correct Option: D

   
   

---

---

95. 

1. 1. 0

   
   
   

   2. ∞

   
   
   

   3. 1 / 2

   
   
   

   4. - ∞

   
   
   

---

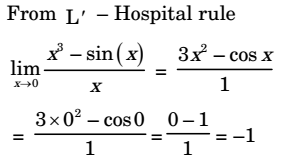
1. View Hint View Answer Discuss in Forum

   
   

   Correct Option: C

   
   

---