Engineering Mathematics Miscellaneous
- The inverse Laplace transform of the function
F (s) = 1 is given by s(s + 1)
-
View Hint View Answer Discuss in Forum
L-1 
1 
= 1 - 1 s(s + 1) s s + 1 L-1 
1 - 1 
= 1 - e-t s s + 1 Correct Option: D
L-1 
1 
= 1 - 1 s(s + 1) s s + 1 L-1 
1 - 1 
= 1 - e-t s s + 1
- The inverse Laplace transform of 1/(s2 + s) is
-
View Hint View Answer Discuss in Forum
1 = 1 = 1 - 1 (s2 + s) s(s + 1) s (s + 1) Correct Option: C
1 = 1 = 1 - 1 (s2 + s) s(s + 1) s (s + 1)
- Evaluation of ∫42 x3 dx using a 2-equal-segment trapezoidal rule gives value of _______.
-
View Hint View Answer Discuss in Forum
Trapezoidal Rule, h = 1

= 1 [ (23 + 43) + 4(33) ] 2 = 1 [ 8 + 64 + 54 ] = 63 2 Correct Option: A
Trapezoidal Rule, h = 1

= 1 [ (23 + 43) + 4(33) ] 2 = 1 [ 8 + 64 + 54 ] = 63 2
- P(0, 3), Q(0.5, 4) and R(1, 5) are three points on the curve defined by f(x). Numerical integration is carried out using both Trapezoidal rule and Simpson's rule within limits x = 0 and x = 1 for the curve. The difference between the two results will be
-
View Hint View Answer Discuss in Forum

By Trapezoidal rule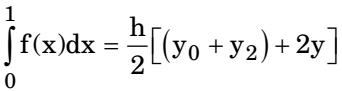
= 0.5 [ (3 + 5) + 2(4) ] = 4 2
By Simpson rule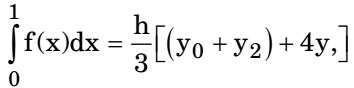
= 0.5 [ (3 + 5) + 4(4) ] = 4 3
Difference between these two results will be 0.Correct Option: A

By Trapezoidal rule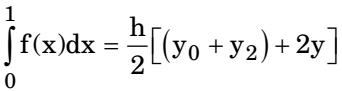
= 0.5 [ (3 + 5) + 2(4) ] = 4 2
By Simpson rule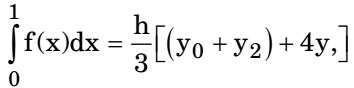
= 0.5 [ (3 + 5) + 4(4) ] = 4 3
Difference between these two results will be 0.
- The error in numerically computing the integral ∫π0 (sinx + cosx) dx using the trapezoidal rule with three intervals of equal length between 0 and π is _________.
-
View Hint View Answer Discuss in Forum


= 2
Error = Exact value – Approx Value
= 2 – 1.8137 = 0.1863Correct Option: B


= 2
Error = Exact value – Approx Value
= 2 – 1.8137 = 0.1863

