Control systems miscellaneous Difficult Questions and Answers | Page - 7

Control systems miscellaneous

In the signal flow graph of figure the gain C/R will be—

1. 11/9
1. 22/15
1. 24/23
1. 44/23

View Hint View Answer Discuss in Forum

By using Manson’s gain formula for signal flow graph.
Here,
P₁ = 2 × 3 × 4 = 24
P₂ = 5
Δ₁ = 1
Δ₂ = 1 – (– 3) = 4
Δ = 1 – (sum of individual loop T. F.) + (sum of loop transmittance products of all possible pairs)
= 1 – (– 2 – 3 – 4 – 5) + (– 2x – 4)
= 1 + 14 + 8
= 23
T.F. = C = P₁Δ₁ + P₂Δ₂
R Δ

= 24 × 1 + 5 × 4
23

= 44
23

Hence alternative (D) is the correct choice.

Correct Option: D

By using Manson’s gain formula for signal flow graph.
Here,
P₁ = 2 × 3 × 4 = 24
P₂ = 5
Δ₁ = 1
Δ₂ = 1 – (– 3) = 4
Δ = 1 – (sum of individual loop T. F.) + (sum of loop transmittance products of all possible pairs)
= 1 – (– 2 – 3 – 4 – 5) + (– 2x – 4)
= 1 + 14 + 8
= 23
T.F. = C = P₁Δ₁ + P₂Δ₂
R Δ

= 24 × 1 + 5 × 4
23

= 44
23

Hence alternative (D) is the correct choice.

The transfer function θ0(s) θ1(s) of the block diagram is

1. G₁G₃G₄
  1 + H₁G₂G₃G₄
1. G₂G₃G₄ + H₂G₄
  1 + H₁G₂G₃G₄
1. G₂G₃G₄ + H₂G₄
  1 + H₁G₂G₃G₄ + H₂G₄H₁
1. G₂G₃G₄ + H₂G₄
  1 + H₁G₂G₃G₄ + H₁H₂G₂G₃G₄

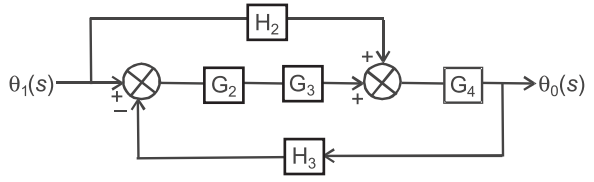
View Hint View Answer Discuss in Forum

Apply same concept as discussed in sol. 136, we get.
Alternative approach
T.F. = θ₀(s) = G₂G₃G₄ + H₂G₄
θ₁(s) 1 + G₂G₃G₄H₁ + H₁H₂G₄

Since, here there are two forward path i.e.,
P₁ = G₂G₃G₄
and P₂ = H₂G₄
and two possible loops i.e.,
L₁ = G₂G₃G₄H₁
and L₂ = H₁H₂G₄
Hence alternative (C) is the correct choice.

Correct Option: C

Apply same concept as discussed in sol. 136, we get.
Alternative approach
T.F. = θ₀(s) = G₂G₃G₄ + H₂G₄
θ₁(s) 1 + G₂G₃G₄H₁ + H₁H₂G₄

Since, here there are two forward path i.e.,
P₁ = G₂G₃G₄
and P₂ = H₂G₄
and two possible loops i.e.,
L₁ = G₂G₃G₄H₁
and L₂ = H₁H₂G₄
Hence alternative (C) is the correct choice.

The overall transfer function O(s)/I(s) is—

1. G₁
  1 + H₁H₃
1. G₁G₂G₃
  1 + G₁G₂G₃H₁H₂H₃
1. G₁G₂G₃
  1 + G₁G₂H₁ + G₂G₃H₂ + G₁G₂G₃ H₃
1. G₁G₂G₃
  1 + G₁G₂G₃H₁ + G₂G₃H₃ + G₁G₂G₃ H₂

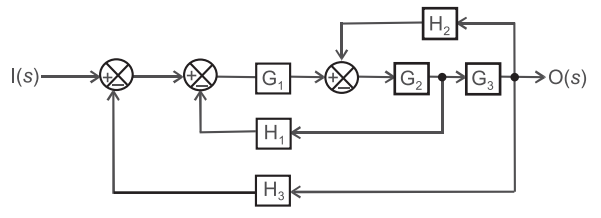
View Hint View Answer Discuss in Forum

In order to calculate the overall transfer function of such type of complex block diagram, use direct formula given below. Overall
T. F. = Sum of total forward path gain
1 + sum of all loops associated with the gain factors

Here, only one forward path = G1G2G3 Sum of all possible loops = G1G2H1 + G1G2G3H3 + G2G3H2 Hence,

O(s) = G₁G₂G₃
I(s) 1 + G₁G₂H₁ + G₁G₂G₃H₃ + G₂G₃H₂

Hence alternative (C) is the correct choice.

Correct Option: C

In order to calculate the overall transfer function of such type of complex block diagram, use direct formula given below. Overall
T. F. = Sum of total forward path gain
1 + sum of all loops associated with the gain factors

Here, only one forward path = G1G2G3 Sum of all possible loops = G1G2H1 + G1G2G3H3 + G2G3H2 Hence,

O(s) = G₁G₂G₃
I(s) 1 + G₁G₂H₁ + G₁G₂G₃H₃ + G₂G₃H₂

Hence alternative (C) is the correct choice.

Consider a closed loop system shown in figure (a) below. The root locus for it is shown in figure (b). The closed-loop transfer function for the system is—

1. K
  1 + (0·5s + 1) (10s + 1)
1. K
  (s + 2) (s + 0·1)
1. K
  1 + K (0·5s + 1) (10s + 1)
1. K
  K + (0·5s + 1) (10s + 1)

View Hint View Answer Discuss in Forum

From root locus, the poles of G(s) lie at s = – 0·1 and s = – 2.
Hence we can have G(s) of the form KG(s) F
= K
(0·5s + 1) (10s + 1)

Hence the closed-loop transfer function
= C(s)
R(s)

= KG(s)
1 + KG(s) H(s)

Since, H(s) = 1, we have
C(s) = KG(s)
R(s) 1 + KG(s)

= K/(0·5s + 1) (10s + 1)
1 + K/(0·5s + 1) (10s + 1)

= K
(0·5s + 1) (10s + 1) + K

Hence (D) is the correct choice.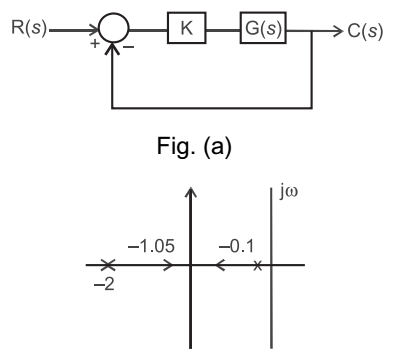

Correct Option: D

From root locus, the poles of G(s) lie at s = – 0·1 and s = – 2.
Hence we can have G(s) of the form KG(s) F
= K
(0·5s + 1) (10s + 1)

Hence the closed-loop transfer function
= C(s)
R(s)

= KG(s)
1 + KG(s) H(s)

Since, H(s) = 1, we have
C(s) = KG(s)
R(s) 1 + KG(s)

= K/(0·5s + 1) (10s + 1)
1 + K/(0·5s + 1) (10s + 1)

= K
(0·5s + 1) (10s + 1) + K

Hence (D) is the correct choice.

129. For what values of ‘a’ does the system shown in figure have a zero steady s`tate error (i.e. Lim t → ∞ e(t)) for a step input?

1. a = 0
1. a > 0
1. a ≥ 4
1. For no value of a

View Hint View Answer Discuss in Forum

From figure Since, E(s) = X(s) – Y(s).H(s)
or E(s) = X(s) – G(s) X(s).H(s)
1 + G(s) H(s)

or E(s) = X(s) – 1
1 + G(s) H(s)

∴ X(s) = 1 for step input
s

or E(s) = 1 1
s +1 (s + 1) × 1/(s² + 5 + a)(s + 4)

Now, steady state error e_ss is
e_ss = _{t → ∞}lim e(t) = _{t → ∞}lim sE(s)

or e_ss = _{s → 0}lim ·s 1 1
s +1 (s + 1) × 1/(s² + 5 + a)(s + 4)

or
or e_ss = 4a
4a + 1

for steady state error, e_ss to be zero,
4a = 0
4a + 1

or
a = 0 Hence alternative (A) is the correct choice.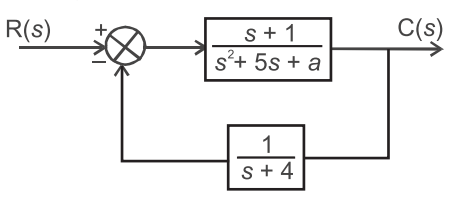

Correct Option: A

From figure Since, E(s) = X(s) – Y(s).H(s)
or E(s) = X(s) – G(s) X(s).H(s)
1 + G(s) H(s)

or E(s) = X(s) – 1
1 + G(s) H(s)

∴ X(s) = 1 for step input
s

or E(s) = 1 1
s +1 (s + 1) × 1/(s² + 5 + a)(s + 4)

Now, steady state error e_ss is
e_ss = _{t → ∞}lim e(t) = _{t → ∞}lim sE(s)

or e_ss = _{s → 0}lim ·s 1 1
s +1 (s + 1) × 1/(s² + 5 + a)(s + 4)

or
or e_ss = 4a
4a + 1

for steady state error, e_ss to be zero,
4a = 0
4a + 1

or
a = 0 Hence alternative (A) is the correct choice.