Control systems miscellaneous
- The overall transfer function of the system in figure is—
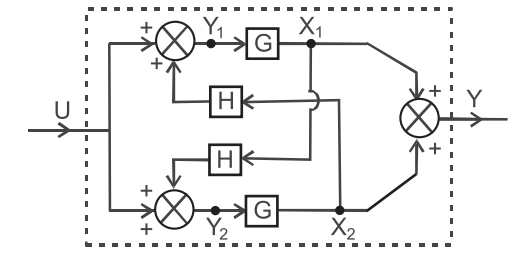
-
View Hint View Answer Discuss in Forum
From given figure
Y1 = U + X2H …(i)
Y2 = U + X1H …(ii)
and
X1 = GY1 = G (U + X2H) = GU + GX2H
X2 = GY2 = G (U + X1H) = GU + GX1H
Now,
Y = X1 + X2
or
Y = GU + GX2H + GU + GX1H
or
Y = 2GU + GH (X1 + X2)
or
Y = 2GU + GHY
or
Y – GHY = 2GU
or
Y/U = 2G/1 – GH
Correct Option: B
From given figure
Y1 = U + X2H …(i)
Y2 = U + X1H …(ii)
and
X1 = GY1 = G (U + X2H) = GU + GX2H
X2 = GY2 = G (U + X1H) = GU + GX1H
Now,
Y = X1 + X2
or
Y = GU + GX2H + GU + GX1H
or
Y = 2GU + GH (X1 + X2)
or
Y = 2GU + GHY
or
Y – GHY = 2GU
or
Y/U = 2G/1 – GH
- The feedback control system shown in the given figure represents a—

-
View Hint View Answer Discuss in Forum
C(s) = (s2/(s + 1))((s + 2)/s4(s + 1)) R(s) 1 + {(s2)/(s + 1)2)}{(s + 2)/s4(s + 1)} × {(2s + 3)/(s + 4)} C(s) = s2(s + 2) R(s) s4(s + 1)3(s + 4) + s2(s + 2)(2s + 3)
orC(s) = (s + 2) R(s) [s2(s + 1)3 (s + 4) + (s + 2) (2s + 3)]
This system that system is type, 0.
Correct Option: A
C(s) = (s2/(s + 1))((s + 2)/s4(s + 1)) R(s) 1 + {(s2)/(s + 1)2)}{(s + 2)/s4(s + 1)} × {(2s + 3)/(s + 4)} C(s) = s2(s + 2) R(s) s4(s + 1)3(s + 4) + s2(s + 2)(2s + 3)
orC(s) = (s + 2) R(s) [s2(s + 1)3 (s + 4) + (s + 2) (2s + 3)]
This system that system is type, 0.
- Transfer function G(s) has the pole-zero as shown in the given figure. Given that the steady state gain is 2, the transfer function G(s) will be given by—
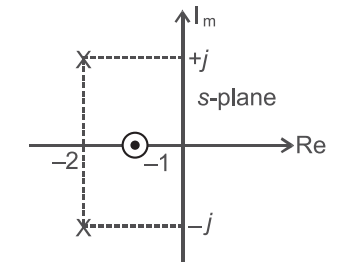
-
View Hint View Answer Discuss in Forum
Here there are 2 pole and 1 zero.
Let the transfer function G (s) of the typeG (s) = K(s + 1) (s + 2 + j) (s + 2 – j) or G (s) = K(s + 1) = K(s + 1) (s + 2)2 – j2 s2 + 4s + 5
Also given that steady state gain is 2.i.e., G (0) = 2 = K (0 + 1) 02 + 4·0 + 5
or
K = 10
Now,the T.F. G (s) = 10 (s + 1) s2 + 4s + 5 
Correct Option: C
Here there are 2 pole and 1 zero.
Let the transfer function G (s) of the typeG (s) = K(s + 1) (s + 2 + j) (s + 2 – j) or G (s) = K(s + 1) = K(s + 1) (s + 2)2 – j2 s2 + 4s + 5
Also given that steady state gain is 2.i.e., G (0) = 2 = K (0 + 1) 02 + 4·0 + 5
or
K = 10
Now,the T.F. G (s) = 10 (s + 1) s2 + 4s + 5 
- Consider the control system shown in the following figure and the statements given below.
1. The system is of second order.
2. Basically, the system is having positive feedback.
3. The system is of type 1.
4. The dimension of the output is not the same as that of the input. Of these statements—
-
View Hint View Answer Discuss in Forum
Here,
G(s) = 9 s (s + 3)
H (s) = – s2 9
T.F. of the given system= G(s) 1 + G(s) H(s) = 9/s(s + 3) 1 + {9/s(s + 3)}(– s2/9)
form, this we conclude that only statement 2 and 4 is correct.= 9 = 3 s2 + 3s – s2 s
Hence alternative (B) is the correct choice.
Correct Option: B
Here,
G(s) = 9 s (s + 3)
H (s) = – s2 9
T.F. of the given system= G(s) 1 + G(s) H(s) = 9/s(s + 3) 1 + {9/s(s + 3)}(– s2/9)
form, this we conclude that only statement 2 and 4 is correct.= 9 = 3 s2 + 3s – s2 s
Hence alternative (B) is the correct choice.
- The transfer function Eo(s)/Ei(s) of the network is

-
View Hint View Answer Discuss in Forum
KCL at node A, and apply Laplace transform
VA(s) – Ei(s) + VA .Cs + VA – E0(s) = 0 …(i) R R
[˙.˙ VB = Eo(s)]
KCL at node B.E0(s) + E0(s) – VA = 0 …(ii) 1/Cs R
from equation (ii)
VA= Eo(s) [RCS + 1] …(iii)
Now by using equations (i) and (iii) and on putting T = RC we getEo (s). [Ts + 1] = Ei(s) + E0(s) (Ts + 2)
oror Eo (s). 
Ts + 1 - 1 
= Ej(s) Ts + 2 (Ts + 2) or E0(s) = 1 Ej(s) T2s2 + 3Ts + 1 
Correct Option: C
KCL at node A, and apply Laplace transform
VA(s) – Ei(s) + VA .Cs + VA – E0(s) = 0 …(i) R R
[˙.˙ VB = Eo(s)]
KCL at node B.E0(s) + E0(s) – VA = 0 …(ii) 1/Cs R
from equation (ii)
VA= Eo(s) [RCS + 1] …(iii)
Now by using equations (i) and (iii) and on putting T = RC we getEo (s). [Ts + 1] = Ei(s) + E0(s) (Ts + 2)
oror Eo (s). 
Ts + 1 - 1 
= Ej(s) Ts + 2 (Ts + 2) or E0(s) = 1 Ej(s) T2s2 + 3Ts + 1 

