Control systems miscellaneous Difficult Questions and Answers | Page - 14

Control systems miscellaneous

For the transfer function
G(s) H(s) = 1
s(s + 1) (s + 0·5)

the phase cross-over frequency is—

1. 0.5 rad/sec
1. 0.707 rad/sec
1. 1.732 rad/sec
1. 2 rad/sec

View Hint View Answer Discuss in Forum

Phase cross-over frequency for the given transfer function
G(s)H(s) = 1
s(s + 1)(s + 0·5)

∠G(s H(s) = – 90° – tan^–1(ω/1) – tan^–1(ω/0.5)
– 180° = – 90° – tan^–1 ω – tan^–1 (2ω)
or 90° = tan^–1 ω + 2ω ⎪_{at ω = ωP}
1 – ω.2ω

or tan 90° = 3ω ⎪_{at ω = ωP}
1 – 2ω²

or 1 = 3ω ⎪_{at ω = ωP}
0 1 – 2ω²

or 1 – 2 ω²_P = 0
or ω_P = 1/√2
ω_P = 0.707 rad/sec.

Correct Option: B

Phase cross-over frequency for the given transfer function
G(s)H(s) = 1
s(s + 1)(s + 0·5)

∠G(s H(s) = – 90° – tan^–1(ω/1) – tan^–1(ω/0.5)
– 180° = – 90° – tan^–1 ω – tan^–1 (2ω)
or 90° = tan^–1 ω + 2ω ⎪_{at ω = ωP}
1 – ω.2ω

or tan 90° = 3ω ⎪_{at ω = ωP}
1 – 2ω²

or 1 = 3ω ⎪_{at ω = ωP}
0 1 – 2ω²

or 1 – 2 ω²_P = 0
or ω_P = 1/√2
ω_P = 0.707 rad/sec.

Consider the system
X(t) = 1 1 X(t) + b₁ u(t)
0 -1 b₂

c (t) = d₁ d₂ X (t)
The conditions for complete state controllability and complete observability is—

1. d₁ > 0, b₂ > 0, b₁ and d₂ can be anything
1. d₁ > 0, b₂ > 0, b₁ and b₂ can be anything
1. b₁ > 0, b₂ > 0, d₁ and d₂ can be anything
1. b₁ > 0, b₂ > 0, b₁ and d₁ can be anything

View Hint View Answer Discuss in Forum

Given
A = 1 1 , B = b₁
0 1 b₂

C=[d₁d₂]
For observability
Q₀ = [C^T: A^T C^T] ≠ 0
where,
C^T = b₁
b₂

A^T = 1 0
1 1

A^T C^T = 1 0
1 1

A^T C^T = 1 0 d₁ = d₁
1 1 d₂ d₁ + d₂

Now,
Q₀ = d₁ d₁ ≠ 0
d₂ d₁ + d₂

or
d₁(d₁ + d₂) - d₁ d₂2 ≠ ≠ 0
or
d₁² + d₁d₂ ≠ 0
or
d₁² ≠ 0
or
d₁ ≠ 0
For controllability
θ_C = [B: A B] ≠ 0
where,
B = d₁
d₂

AB = 1 1 d₁ = d₁ + d₂
0 1 d₂ d₂

or
Q_c = d₁ d₁ + d₂
d₂ d₂

or
b₁ b₂ – b₂ (b₁ + b₂) ≠ 0
or
b₁ b₂ – b₂² – b₁ b₂ ≠ 0
or
– b₂² ≠ 0
or
b₂ ≠ 0
Finally we conclude that only option (A) fulfils this condition.

Correct Option: A

Given
A = 1 1 , B = b₁
0 1 b₂

C=[d₁d₂]
For observability
Q₀ = [C^T: A^T C^T] ≠ 0
where,
C^T = b₁
b₂

A^T = 1 0
1 1

A^T C^T = 1 0
1 1

A^T C^T = 1 0 d₁ = d₁
1 1 d₂ d₁ + d₂

Now,
Q₀ = d₁ d₁ ≠ 0
d₂ d₁ + d₂

or
d₁(d₁ + d₂) - d₁ d₂2 ≠ ≠ 0
or
d₁² + d₁d₂ ≠ 0
or
d₁² ≠ 0
or
d₁ ≠ 0
For controllability
θ_C = [B: A B] ≠ 0
where,
B = d₁
d₂

AB = 1 1 d₁ = d₁ + d₂
0 1 d₂ d₂

or
Q_c = d₁ d₁ + d₂
d₂ d₂

or
b₁ b₂ – b₂ (b₁ + b₂) ≠ 0
or
b₁ b₂ – b₂² – b₁ b₂ ≠ 0
or
– b₂² ≠ 0
or
b₂ ≠ 0
Finally we conclude that only option (A) fulfils this condition.

The value of A matrix in X′ = AX for the system described by the differential equation ÿ + 2y · + 3y = 0 is—

1. 1 0
  -2 -1
1. 1 0
  -1 -2
1. 0 1
  -2 -1
1. 1 0
  -3 -2

View Hint View Answer Discuss in Forum

Try yourself

Correct Option: D

Try yourself

The state and output equation of a system are as under state equation:
x₁ (t) = 0 1 x₁ (t) + 0 u(t)
x₂ (t) -1 -2 x₂ (t) 1

And
C(t) =[1 1] x₁ (t)
x₂ (t)

The system is—

1. neither state controllable nor output controllable
1. state controllable but not output controllable
1. output controllable but not state controllable
1. both state controllable and output controllable

View Hint View Answer Discuss in Forum

Given state equation:
x₁ (t) = 0 1 x₁ (t) + 0 u(t)
x₂ (t) -1 -2 x₂ (t) 1

C(t) = [1 1] x₁ (t)
x₂ (t)

Here,
A = 0 1
-1 -2

B = 0
1

C = [1 1]
Check for controllability
AB = 0 1 0 = 1
-1 -2 1 -2

∴ Q_C = [B: AB] = – 1, which is non-singular.
Hence, the state equation is controllable.
Check for observability :
A = 0 1
-1 -2

then
A^T = 0 -1
1 -2

C = [1 1]
then
C^T = 1
1

Now,
A^TC^T = 0 -1 1
1 -2 1

= -1
-1

θ₀ = [C^T : A^T C^T]
A^TC^T = 1 -1
1 -1

= 0 i.e., singular.
Hence given system equation is not observable.
Therefore alternative (B) is the correct choice.

Correct Option: B

Given state equation:
x₁ (t) = 0 1 x₁ (t) + 0 u(t)
x₂ (t) -1 -2 x₂ (t) 1

C(t) = [1 1] x₁ (t)
x₂ (t)

Here,
A = 0 1
-1 -2

B = 0
1

C = [1 1]
Check for controllability
AB = 0 1 0 = 1
-1 -2 1 -2

∴ Q_C = [B: AB] = – 1, which is non-singular.
Hence, the state equation is controllable.
Check for observability :
A = 0 1
-1 -2

then
A^T = 0 -1
1 -2

C = [1 1]
then
C^T = 1
1

Now,
A^TC^T = 0 -1 1
1 -2 1

= -1
-1

θ₀ = [C^T : A^T C^T]
A^TC^T = 1 -1
1 -1

= 0 i.e., singular.
Hence given system equation is not observable.
Therefore alternative (B) is the correct choice.

Obtain the transfer function for the response curve shown below—

1. 40
  s(1 + 0·1s)
1. 4
  s(1 + 0·1s)
1. 4
  s(1 + 0·01s)
1. 20
  s(1 + 0·1s)

View Hint View Answer Discuss in Forum

From figure
20 log₁₀ K = 12
K = 10^12/20
or K = 3·98 ≈ 4
one pole atω = 100
i.e., (1 + sT),
where
T₀ = 1/ω = 1/100
(1 + 0·01s)
Hence transfer function, G(s) H(s) = 4/1 + 0·01s
Hence alternative (C) is the correct choice.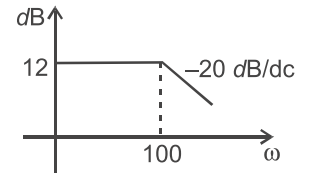

Correct Option: C

From figure
20 log₁₀ K = 12
K = 10^12/20
or K = 3·98 ≈ 4
one pole atω = 100
i.e., (1 + sT),
where
T₀ = 1/ω = 1/100
(1 + 0·01s)
Hence transfer function, G(s) H(s) = 4/1 + 0·01s
Hence alternative (C) is the correct choice.