Control systems miscellaneous
- The root locus plot is shown below. What is the transfer function?

-
View Hint View Answer Discuss in Forum
From root locus plot it is clear that there are 4 asymptotes with angles 45°, 135°, 225° and 315°. and from equation
± (2K + 1) ×180° p – z
where K = 0, 1, 2, 3. suggest 4 poles and no zeros.Centroid; σ = ∑ poles – ∑ zeros p – z = – 1 – 1 – 1 – 1 – 0 = - 1 4
SoT.F. = 4 (as K = 4 is given) (s + 1)4 
Correct Option: D
From root locus plot it is clear that there are 4 asymptotes with angles 45°, 135°, 225° and 315°. and from equation
± (2K + 1) ×180° p – z
where K = 0, 1, 2, 3. suggest 4 poles and no zeros.Centroid; σ = ∑ poles – ∑ zeros p – z = – 1 – 1 – 1 – 1 – 0 = - 1 4
SoT.F. = 4 (as K = 4 is given) (s + 1)4 
- The transfer function has a log-magnitude plot as shown below. Under the assumption that a minimum phase function, its transfer function is—

-
View Hint View Answer Discuss in Forum
From figure transfer function is of the form
K = (one pole) (1 + sT)
as there is 20 dB/dec at
log ω = – 1
or
ω = 1/10
T = 1/ω = 10
Now, log |G| = 1
or
| G | = 10
orK = 10 (10ω)2 + 1
orK = 10 √(10×1/10)2 + 1
orK = 10 √2
k = 10√2
Now,T.F. = 10√2 s·10 + 1
orT.F. = √2 s + 0.1 
Correct Option: D
From figure transfer function is of the form
K = (one pole) (1 + sT)
as there is 20 dB/dec at
log ω = – 1
or
ω = 1/10
T = 1/ω = 10
Now, log |G| = 1
or
| G | = 10
orK = 10 (10ω)2 + 1
orK = 10 √(10×1/10)2 + 1
orK = 10 √2
k = 10√2
Now,T.F. = 10√2 s·10 + 1
orT.F. = √2 s + 0.1 
- The transfer function of a closed loop system is 1/1 + sT. The input to this system is t u(t). The output would track this system, but the error would be—
-
View Hint View Answer Discuss in Forum
Given that
C(s) = 1 R(s) 1 + sT
r(t) = tu(t)
then
R (s) = 1 s/2
E (s) = R (s) – C (s)1 - 1 1 s2 s2 sT + 1 = sT + 1 – 1 s2(sT + 1) = T s(sT + 1)
ess = s → 0Lim . s. E (s)= s → 0Lim s· T = T s(sT + 1)
Correct Option: C
Given that
C(s) = 1 R(s) 1 + sT
r(t) = tu(t)
then
R (s) = 1 s/2
E (s) = R (s) – C (s)1 - 1 1 s2 s2 sT + 1 = sT + 1 – 1 s2(sT + 1) = T s(sT + 1)
ess = s → 0Lim . s. E (s)= s → 0Lim s· T = T s(sT + 1)
- Match List-I with List-II and select the correct answer using the codes given below the lists:

-
View Hint View Answer Discuss in Forum
In order to solve such type of problems, it will be better to calculate the phase at ω = 0 and ω = ∞ with the help of given transfer function.
1.T.F = K (1 + sT1)(1 + sT2)
φ = – tan–1 ωT1 – tan–1 ωT2
φ = 0 at ω = 0
φ = – 90° – 90° = – 180° at ω = ∞
matching with option (C)
i.e., C – 1 which is given in alternative (A) only.
Hence there is no need to solve further.
Hence alternative (A) is the correct answer.Correct Option: A
In order to solve such type of problems, it will be better to calculate the phase at ω = 0 and ω = ∞ with the help of given transfer function.
1.T.F = K (1 + sT1)(1 + sT2)
φ = – tan–1 ωT1 – tan–1 ωT2
φ = 0 at ω = 0
φ = – 90° – 90° = – 180° at ω = ∞
matching with option (C)
i.e., C – 1 which is given in alternative (A) only.
Hence there is no need to solve further.
Hence alternative (A) is the correct answer.
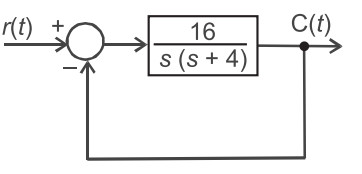
- In the system shown in the given figure, r (t) = sin ωt. The steady-state response c(t) will exhibit a resonance peak at a frequency of—

-
View Hint View Answer Discuss in Forum
From given figure
C(s) = 16 R(s) s2 + 4s + 16
C.E. = s2 + 4s + 16.
on comparing this equation with the standard equation
s2 + 2 ξ ωns + ωn2 = 0
2 ξ ωn = 4 …(i)
ωn2 = 16 …(ii)
resonance peak frequency is given by
ωr = ωn √1 - 2ξ 2
from equations (i) and (ii)
ξ = 0.5
ωn = 4
Thus, ωr = 4√1 – 2(0·5)2
= 2√2.
Correct Option: B
From given figure
C(s) = 16 R(s) s2 + 4s + 16
C.E. = s2 + 4s + 16.
on comparing this equation with the standard equation
s2 + 2 ξ ωns + ωn2 = 0
2 ξ ωn = 4 …(i)
ωn2 = 16 …(ii)
resonance peak frequency is given by
ωr = ωn √1 - 2ξ 2
from equations (i) and (ii)
ξ = 0.5
ωn = 4
Thus, ωr = 4√1 – 2(0·5)2
= 2√2.