56. The 3-dB bandwidth of a typical second-order system with the transfer function
    

    C(s)	=	ω2n
    R(s)		s2 + 2ξ ωns + ω2n

    
    is given by—

1. 1. ω_n√1-2ξ²
      

   
   
   

   2. ω_n√ω² + √ξ⁴ – ξ² + 1

   
   
   

   3. ω_n√(1 – 2ξ²) + √4ξ⁴ - 4ξ³ + 2

   
   
   

   4. ω_n√(1 – 2ξ²) - √4ξ⁴ - 4ξ³ + 2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Refer synopsis.

   Correct Option: C

   Refer synopsis.

---

57. Two identical first-order systems have been cascaded non-interactively. The unit step response of the systems will be—
    

1. 1. overdamped
      

   
   
   

   2. underdamped
      

   
   
   

   3. undamped
      

   
   
   

   4. critically damped

   
   
   

---

1. View Hint View Answer Discuss in Forum

   According to the equation, two identical first order systems have been cascaded non-interactively
   i.e.,
   (1 + sT) (1 + sT)
   C.E. (1 + sT) (1 + sT) = 0
   ⇒ s²T² + 2sT + 1 = 0
   

   ⇒ s2 +	2s	+	1	= 0
   	T		T2

   
   2ξ ωn = 2/T
   ω_n² = 1/T²
   or
   ω_n = 1/T
   

   ξ =	1	=	1	= 1
   	Tωn		T(1/T)

   
   Hence alternative (D) is the correct choice.

   Correct Option: D

   According to the equation, two identical first order systems have been cascaded non-interactively
   i.e.,
   (1 + sT) (1 + sT)
   C.E. (1 + sT) (1 + sT) = 0
   ⇒ s²T² + 2sT + 1 = 0
   

   ⇒ s2 +	2s	+	1	= 0
   	T		T2

   
   2ξ ωn = 2/T
   ω_n² = 1/T²
   or
   ω_n = 1/T
   

   ξ =	1	=	1	= 1
   	Tωn		T(1/T)

   
   Hence alternative (D) is the correct choice.

---

---

58. An integral controller is used to improve the transient response of a first order system. If G (s) = 1/1 + s and the system is operated in closed-loop with unity feedback, what is the value of T_i if integral controller transfer function is 1/T_i s to provide damping ratio of 0.5?
    

1. 1. 0.5
      

   
   
   

   2. 2
      

   
   
   

   3. 1
      

   
   
   

   4. 4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   According to question C.E. of the system 1 + G(s) H(s) = 0
   

   1 +	1	×	1	= 0
   	Tis		1 + s

   
   T_is + T_i s² + 1 = 0
   or
   s² + s + 1/T_i = 0 …(i)
   on comparing equation (i) with the standard equation
   s² + 2ξω_n s + ω_n² = 0
   2ξω_n = 1
   and
   ω_n² = 1/T_i
   or
   ω_n = 1/√T₂
   or
   ξ = 1/2ω_n
   or
   ξ = √T_i/2
   or
   0·5 = √T₁/2
   or
   T_i = 1
   

   
   

   Correct Option: C

   According to question C.E. of the system 1 + G(s) H(s) = 0
   

   1 +	1	×	1	= 0
   	Tis		1 + s

   
   T_is + T_i s² + 1 = 0
   or
   s² + s + 1/T_i = 0 …(i)
   on comparing equation (i) with the standard equation
   s² + 2ξω_n s + ω_n² = 0
   2ξω_n = 1
   and
   ω_n² = 1/T_i
   or
   ω_n = 1/√T₂
   or
   ξ = 1/2ω_n
   or
   ξ = √T_i/2
   or
   0·5 = √T₁/2
   or
   T_i = 1
   

   
   

---

59. A control system is as shown in the given figure. The maximum value of gain K for which the system is stable is—
    
    
    
    

1. 1. √ 3
      

   
   
   

   2. 3
      

   
   
   

   3. 4
      

   
   
   

   4. 5

   
   
   

---

1. View Hint View Answer Discuss in Forum

   C(s)	=	K.(1/s3 + 3s2 + 2s + 1)
   R(s)		1 + (1/s3 + 3s2 + 2s + 1)× 1

   
   and C.E = 1 + G(s) H(s)
   

   ⇒ + 1	K	. 1 = 0
   	s3 + 3s2 + 2s + 1

   
   ⇒ s³ + 3s² + 2s + 1 K = 0
   The Hurwitz criterion can be given as
   s³ 1 2
   s² 3 1 + K
   s³ 6 – (1 + K)/3 0
   s⁰ 1 + K 0
   for the system to be stable
   

   6 – (1 + K)	≥ 0
   3

   
   and
   1 + K ≥ 0
   6 ≥ 1 + K
   or
   1 + K ≤ 6
   or
   K ≤ 5
   K_max = 5

   
   

   Correct Option: D

   C(s)	=	K.(1/s3 + 3s2 + 2s + 1)
   R(s)		1 + (1/s3 + 3s2 + 2s + 1)× 1

   
   and C.E = 1 + G(s) H(s)
   

   ⇒ + 1	K	. 1 = 0
   	s3 + 3s2 + 2s + 1

   
   ⇒ s³ + 3s² + 2s + 1 K = 0
   The Hurwitz criterion can be given as
   s³ 1 2
   s² 3 1 + K
   s³ 6 – (1 + K)/3 0
   s⁰ 1 + K 0
   for the system to be stable
   

   6 – (1 + K)	≥ 0
   3

   
   and
   1 + K ≥ 0
   6 ≥ 1 + K
   or
   1 + K ≤ 6
   or
   K ≤ 5
   K_max = 5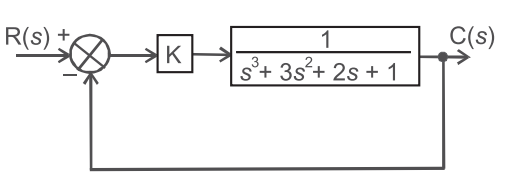

   
   

---

---

60. The open loop transfer function of a unity feedback control system is given by:
    

    G(s) =	K
    	s(s + 1)

    
    If the gain K is increased to infinity, then the damping ratio will tend to become—
    

1. 1. 1/√2
      

   
   
   

   2. 1
      

   
   
   

   3. 0
      

   
   
   

   4. ∞

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given G(s) = K/s(s + 1)
   and
   H(s) = 1
   C.E. 1 + G(s) H(s) = 0
   

   1 +	K	· 1 = 0
   	s(s + 1)

   
   s² + s + K = 0 …(i)
   on comparing equation (i) with the standard equation
   s² + 2ξω_n s + ω_n² = 0,
   we get
   ω_n² = K
   ⇒ ωn = ± √K
   2ξω_n = 1
   or ξ = 1 2√K
   Now, as K → ∞, then ξ → 0.
   Hence alternative (C) is the correct choice.

   Correct Option: C

   Given G(s) = K/s(s + 1)
   and
   H(s) = 1
   C.E. 1 + G(s) H(s) = 0
   

   1 +	K	· 1 = 0
   	s(s + 1)

   
   s² + s + K = 0 …(i)
   on comparing equation (i) with the standard equation
   s² + 2ξω_n s + ω_n² = 0,
   we get
   ω_n² = K
   ⇒ ωn = ± √K
   2ξω_n = 1
   or ξ = 1 2√K
   Now, as K → ∞, then ξ → 0.
   Hence alternative (C) is the correct choice.

---