Control systems miscellaneous Difficult Questions and Answers | Page - 15

Control systems miscellaneous

A unity feedback system has an open loop transfer function, G(s) = K/s>sup>2. The root locus plot is—

1. Fig:- A
1. Fig:- B
1. Fig:- C
1. Fig:- D

View Hint View Answer Discuss in Forum

G(s) = K/s²
Angle of asymptote,
φ_A = ± (2q + 1)180
2 – 0

where, q = 0, 1
when q = 0
φ_A = 90°
and when q = 1, φ_A = 270°
Hence root locus given in option (B) correct choice.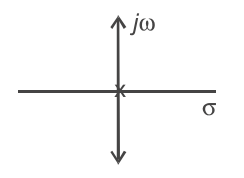

Correct Option: B

G(s) = K/s²
Angle of asymptote,
φ_A = ± (2q + 1)180
2 – 0

where, q = 0, 1
when q = 0
φ_A = 90°
and when q = 1, φ_A = 270°
Hence root locus given in option (B) correct choice.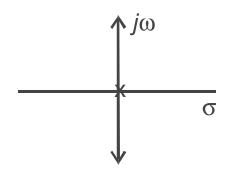

A unity feedback system has open-loop T.F. is G(s) = {25/ [s (s + 6)]}. The peak overshoot in the step-input response of the system is approximately equal to—

1. 5%
1. 10%
1. 15%
1. 20%

View Hint View Answer Discuss in Forum

Given G(s) = 25 , H(s) = 1
s(s + 6)

the C.E. = 1 + G(s) H(s) = 0
= 1 + 25/s(s + 6) · 1 = 0
= s² + 6s + 25 = 0
Here, ω²_n = 25
⇒ ω_n = ± 5
2ξω_n = 6
or ξ = 6/2 × 5 = ·6
Now,% maximum overshoot, M_P
e^{-πξ/√1-(0.6)²}×100
e^{-0.6π/√1-(0.6)²}×100
= 10%

Correct Option: B

Given G(s) = 25 , H(s) = 1
s(s + 6)

the C.E. = 1 + G(s) H(s) = 0
= 1 + 25/s(s + 6) · 1 = 0
= s² + 6s + 25 = 0
Here, ω²_n = 25
⇒ ω_n = ± 5
2ξω_n = 6
or ξ = 6/2 × 5 = ·6
Now,% maximum overshoot, M_P
e^{-πξ/√1-(0.6)²}×100
e^{-0.6π/√1-(0.6)²}×100
= 10%

The maximum phase shift that can be obtained by using a lead compensator with transfer function
G(s) = (1 + 0.15s)
(1 + 0.05s)

is equal to—

1. 15°
1. 30°
1. 45°
1. 60°

View Hint View Answer Discuss in Forum

Given, G(s) = (1 + 0·15s) ......…(i)
(1 + 0·05s)

In phase lead compensation.
Given, G(s) = V₀(s) = (1 + sT) ......…(ii)
V_i(s) (1 + sαT)

on comparing equations (i) and (ii), we have
T = 0·15
αT = 0·05
or
α = 0·05/0·15 = 1/3
Now,
sin φ_m = 1 – α
1 + α

where, φ_m is the maximum phase shift angle
or
sin φ_m = 1 – (1/3)
1 + (1/3)

or
sin φ_m = 2/4 = 1/2
or
φ_m = sin^–1 (1/2) = 30°
Hence alternative (B) is the correct choice.

Correct Option: B

Given, G(s) = (1 + 0·15s) ......…(i)
(1 + 0·05s)

In phase lead compensation.
Given, G(s) = V₀(s) = (1 + sT) ......…(ii)
V_i(s) (1 + sαT)

on comparing equations (i) and (ii), we have
T = 0·15
αT = 0·05
or
α = 0·05/0·15 = 1/3
Now,
sin φ_m = 1 – α
1 + α

where, φ_m is the maximum phase shift angle
or
sin φ_m = 1 – (1/3)
1 + (1/3)

or
sin φ_m = 2/4 = 1/2
or
φ_m = sin^–1 (1/2) = 30°
Hence alternative (B) is the correct choice.

In the network shown in the given figure. If the voltage V at the time considered is 20 V, then dV/dt at that time will be—

1. 1 V/s
1. 2 V/s
1. – 2 V/s
1. Zero

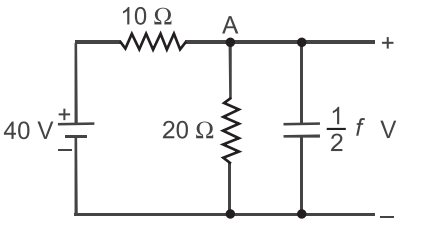
View Hint View Answer Discuss in Forum

From figure, the current through
20Ω resistor = 20/20 = 1A.
current through 10Ω resistor
= 40 – 20/10 = 2A.
By applying KCL at point A, current in the capacitor, say
i = 2 – 1 = 1A.
As we know that current across capacitor is given by relation

i = C dV
dt

i = 1 dV
2 dt

or
or dV = 2V/s
dt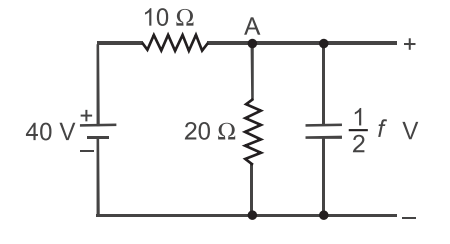

Correct Option: B

From figure, the current through
20Ω resistor = 20/20 = 1A.
current through 10Ω resistor
= 40 – 20/10 = 2A.
By applying KCL at point A, current in the capacitor, say
i = 2 – 1 = 1A.
As we know that current across capacitor is given by relation

i = C dV
dt

i = 1 dV
2 dt

or
or dV = 2V/s
dt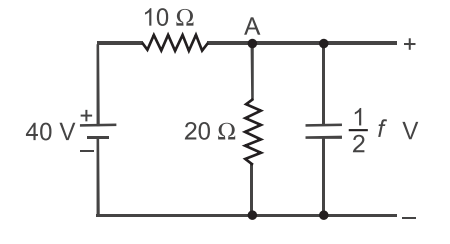

If the unit step response of a network is (1 – e^–αt), then its unit impulse response will be—

1. α e^–αt
1. α e^–t/α
1. 1/α e^–αt
1. (1 – α) e^–αt

View Hint View Answer Discuss in Forum

Given the unit step response is 1– e^–αt, means
If r(t) = u(t)
then
R(s) = 1/s
y(t) = 1 – e^–αt then
Y(s) = 1/s – 1/s + α = α/s(s + α)
Therefore, the transfer function of the system,
H(s) = Y(s)
R(s)

= Y(s)
s(s + α) 1/s

= α
s + α

Now, for input, r(t) = δ (t)
i.e., R(s) = 1
Y(s) = H(s) R(s)
or
Y(s) = α ·1
s + α

or
Y(t) = α·e^–αt
Alternative method: Unit impulse response of a linear, time invariant network is the derivative of unit step function response of the network. Unit step response is (1 – e^–αt)
∴ Unit impulse response is – (– α) e^–αt = αe^–αt

Correct Option: A

Given the unit step response is 1– e^–αt, means
If r(t) = u(t)
then
R(s) = 1/s
y(t) = 1 – e^–αt then
Y(s) = 1/s – 1/s + α = α/s(s + α)
Therefore, the transfer function of the system,
H(s) = Y(s)
R(s)

= Y(s)
s(s + α) 1/s

= α
s + α

Now, for input, r(t) = δ (t)
i.e., R(s) = 1
Y(s) = H(s) R(s)
or
Y(s) = α ·1
s + α

or
Y(t) = α·e^–αt
Alternative method: Unit impulse response of a linear, time invariant network is the derivative of unit step function response of the network. Unit step response is (1 – e^–αt)
∴ Unit impulse response is – (– α) e^–αt = αe^–αt