The transfer function θ0(s) θ1(s) of the block diagram

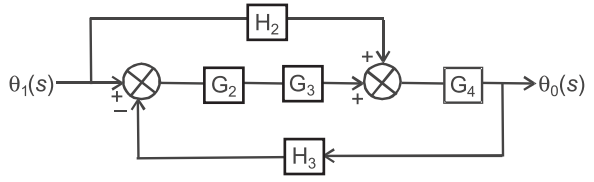
Home » Control Systems » Control systems miscellaneous » Question

The transfer function θ0(s) θ1(s) of the block diagram is

1. G₁G₃G₄
  1 + H₁G₂G₃G₄
2. G₂G₃G₄ + H₂G₄
  1 + H₁G₂G₃G₄
3. G₂G₃G₄ + H₂G₄
  1 + H₁G₂G₃G₄ + H₂G₄H₁
4. G₂G₃G₄ + H₂G₄
  1 + H₁G₂G₃G₄ + H₁H₂G₂G₃G₄

Correct Option: C

Apply same concept as discussed in sol. 136, we get.
Alternative approach

T.F. =	θ₀(s)	=	G₂G₃G₄ + H₂G₄
	θ₁(s)		1 + G₂G₃G₄H₁ + H₁H₂G₄

Since, here there are two forward path i.e.,
P₁ = G₂G₃G₄
and P₂ = H₂G₄
and two possible loops i.e.,
L₁ = G₂G₃G₄H₁
and L₂ = H₁H₂G₄
Hence alternative (C) is the correct choice.