Sets and Functions
- In a group of 1000 people, there are 750 people who can speak Hindi and 400 who can speak English. How many can speak Hindi only?
-
View Hint View Answer Discuss in Forum
Given in the question,
n(H ∪ E) = 1000, n(H) = 750, n(E) = 400
Use the below formula,
n(H ∪ E) = n(H) + n(E) – n(H ∩ E)Correct Option: A
Given in the question,
n(H ∪ E) = 1000, n(H) = 750, n(E) = 400
Use the below formula,
n(H ∪ E) = n(H) + n(E) – n(H ∩ E)
We get 1000 = 750 + 400 – n(H ∩ E)
⇒ n(H ∩ E) = 1150 – 1000 = 150.
Number of People who can speak Hindi only
= n(H ∩ E′) = n(H) – n(H ∩ E)
= 750 – 150 = 600.
- In a group of 70 people, 37 like coffee, 52 like tea and each person likes at least one of the two drinks. How many people like both coffee and tea?
-
View Hint View Answer Discuss in Forum
Let P = set of people who like coffee and Q = set of people like tea.
Then, P ∪ Q = set of people who like at least one of the two drinks.
And P ∩ Q = set of people who like both the drinks.Correct Option: A
Let P = set of people who like coffee and Q = set of people like tea.
Then, P ∪ Q = set of people who like at least one of the two drinks.
And P ∩ Q = set of people who like both the drinks.
Given in the question,
n(P) = 37, n(Q) = 52, n(P ∪ Q) = 70.
Use the below formula,
n(P ∪ Q) = n(P) + n(Q) – n(P ∩ Q)
Put the value from the given question,
70 = 37 + 52 – n(P ∩ Q)
⇒ n(P ∩ Q) = 89 – 70 = 19.
∴ 19 people like both coffee and tea.
- In a town with a population of 5000, 3200 people are egg-eaters, 2500 meat eaters and 1500 eat both egg and meat. How many are pure vegetarians?
-
View Hint View Answer Discuss in Forum
Let, E be the set of people who are egg-eaters and M be the set of people who are meat-eaters.
As per given question,
n(E) = 3200, n(M) = 2500, n(E ∩ M) = 1500.
Use the formula
n(E ∪ M) = n(E) + n(M) – n(E ∩ M)
Number of pure vegetarians = n(U) – n(E ∪ M)Correct Option: B
Let, E be the set of people who are egg-eaters and M be the set of people who are meat-eaters.
As per given question,
n(E) = 3200, n(M) = 2500, n(E ∩ M) = 1500.
Use the formula
n(E ∪ M) = n(E) + n(M) – n(E ∩ M)
= 3200 + 2500 – 1500
= 5700 – 1500 = 4200.
∴ Number of pure vegetarians = n(U) – n(E ∪ M)
Number of pure vegetarians = 5000 – 4200 = 800.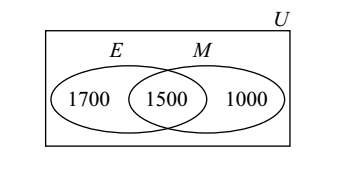
- If A = {a, d}, B = {b, c, e} and C = {b, c, f}, then A × (B ∪ C) =
-
View Hint View Answer Discuss in Forum
Given in the question,
(B ∪ C) = {b, c, e} ∪ {b, c, f} = {b, c, e, f}
∴ A × (B ∪ C) = {a, d} × {b, c, e, f}Correct Option: C
As per given question,
(B ∪ C) = {b, c, e} ∪ {b, c, f} = {b, c, e, f}
∴ A × (B ∪ C) = {a, d} × {b, c, e, f}
= {(a, b), (a, c), (a, e), (a, f), (d, b), (d, c), (d, e), (d, f)} …...........(1)
Also, (A × B) = {(a, b), (a, c), (a, e), (d, b), (d, c), (d, e)}
and, (A × C) = {(a, b), (a, c), (a, f), (d, b), (d, c), (d, f)} …............(2)
∴ (A × B) ∪ (A × C) = {(a, b), (a, c), (a, e), (a, f), (d, b), (d, c), (d, e), (d, f)}
From (1) and (2), we have
A × (B ∪ C) = (A × B) ∪ (A × C).
- If A and B are two sets such that A has 40 elements, A ∪ B has 60 elements and A ∪ B has 10 elements, how many elements does B have?
-
View Hint View Answer Discuss in Forum
Given in the question ,
n(A) = 40, n(A ∩ B) = 60 and n(A ∩ B) = 10.
Putting these values in the formula
n(A ∪ B) = n(A) + n(B) – n(A ∩ B) we get
60 = 40 + n(B) − 10
⇒ n(B) = 30.Correct Option: B
Given in the question ,
n(A) = 40, n(A ∩ B) = 60 and n(A ∩ B) = 10.
As we know the formula,
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
Putting these values in the formula, we get
60 = 40 + n(B) − 10
⇒ n(B) = 30.

