16. A band brake having bandwidth of 80 mm, drum diameter of 250 mm, coefficient of friction of 0.25 and angle of wrap of 270 degrees is required to exert a friction torque of 1000 N m. The maximum tension (in kN) developed in the band is

1. 1. 1.88

   
   
   

   2. 3.56

   
   
   

   3. 6.12

   
   
   

   4. 11.56

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given: b = 80 mm = 0.08 m D = 250 mm = 0.25
   

   R =	D	= 0.25
   	2

   
   μ = 0.25
   

   θ = 270° = 270 ×	π	= 4.712 radians
   	180

   
   F_t = 100 N-m
   

   As	p1	= eμθ
   	p2

   
   ⇒  p₁ = e^μθ ⋅ p₂ = e^{0.25 × 4.712} ⋅ p₂ = 3.25p₂
   Now, F_t = (p₁ − p₂)R
   

   ∴  1000 =		p1 −	p1		0.125
   			3.25

   
   Solving, we get maximum tension in the belt,
   p₁ = 11.56 kN

   Correct Option: D

   Given: b = 80 mm = 0.08 m D = 250 mm = 0.25
   

   R =	D	= 0.25
   	2

   
   μ = 0.25
   

   θ = 270° = 270 ×	π	= 4.712 radians
   	180

   
   F_t = 100 N-m
   

   As	p1	= eμθ
   	p2

   
   ⇒  p₁ = e^μθ ⋅ p₂ = e^{0.25 × 4.712} ⋅ p₂ = 3.25p₂
   Now, F_t = (p₁ − p₂)R
   

   ∴  1000 =		p1 −	p1		0.125
   			3.25

   
   Solving, we get maximum tension in the belt,
   p₁ = 11.56 kN

---

17. A force of 400 N is applied to the brake drum of 0.5 m diameter in a band brake system as shown in figure, where the wrapping angle is 180°. If the coefficient of friction between the drum and the band is 0.25, the braking torque applied, in Nm is
    

1. 1. 100.6

   
   
   

   2. 54.4

   
   
   

   3. 22.1

   
   
   

   4. 15.7

   
   
   

---

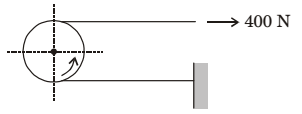
1. View Hint View Answer Discuss in Forum

   
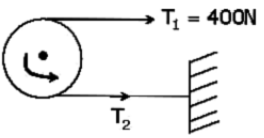
   As the drum is rotating in anti clock wise direction, T₁ will be right side & T₂ will be clock side.
   

   T1	= eμθ = e0.25 × π = 2.19
   T2

   
   ⇒  T₂ = = 182.375 N
   Braking torque = (T₁ – T₂ )r
   = 54.4 N – m

   Correct Option: B

   
   As the drum is rotating in anti clock wise direction, T₁ will be right side & T₂ will be clock side.
   

   T1	= eμθ = e0.25 × π = 2.19
   T2

   
   ⇒  T₂ = = 182.375 N
   Braking torque = (T₁ – T₂ )r
   = 54.4 N – m

---

---

18. A drum brake is shown in the figure. The drum is rotating in anticlockwise direction. The coefficient of friction between drum and shoe is 0.2. The dimensions shown in the figure are in mm. The braking torque (in Nm) for the brake shoe is________.
    

1. 1. 64 N - M

   
   
   

   2. 24 N - M

   
   
   

   3. 11 N - M

   
   
   

   4. None of the above

   
   
   

---

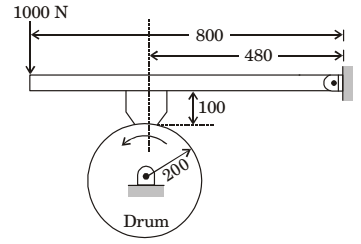
1. View Hint View Answer Discuss in Forum

   Taking moments about pin joint (SM)
   ⇒  1000 × 0.8 =R_N × 0.48 + μR_N × 0.1
   

   ⇒  RN =	800	= 1600
   	0.5

   
   T_B = μR_N × r
   

   = 0.2 × 1600 ×	200	= 64 N - M
   	1000

   Correct Option: A

   Taking moments about pin joint (SM)
   ⇒  1000 × 0.8 =R_N × 0.48 + μR_N × 0.1
   

   ⇒  RN =	800	= 1600
   	0.5

   
   T_B = μR_N × r
   

   = 0.2 × 1600 ×	200	= 64 N - M
   	1000

---

19. In spur gears, the circle on which the involute is generated is called the

1. 1. pitch circle

   
   
   

   2. clearance angle

   
   
   

   3. base circle

   
   
   

   4. addendum circle

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: C

   NA

---

---

20. The forces F₁ and F₂ in a brake band and the direction of rotation of the drum are as shown in the figure. The coefficient of friction is 0.25. The angle of wrap is 3π/2 radians. It is given that R = 1 m and F2 = 1 N. The torque (in Nm) exerted on the drum is ________ .
    

1. 1. 2.8 N-m

   
   
   

   2. .248 N-m

   
   
   

   3. 2.248 N-m

   
   
   

   4. None of the above

   
   
   

---

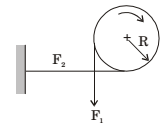
1. View Hint View Answer Discuss in Forum

   	F1	= e μ θ = e 0.25 × (3π / 2) = 3.248
   	F2

   
   ∴ F₁ = 3.248 N
   Torque, T = (F₁ – F₂) × r
   = (3.248 – 1) × 1 = 2.248 N-m

   Correct Option: C

   	F1	= e μ θ = e 0.25 × (3π / 2) = 3.248
   	F2

   
   ∴ F₁ = 3.248 N
   Torque, T = (F₁ – F₂) × r
   = (3.248 – 1) × 1 = 2.248 N-m

---