Machine Design Miscellaneous
- A bar is subjected to fluctuating tensile load from 20 kN to 100 kN. The material has yield strength of 240 MPa and endurance limit in reversed bending is 160 MPa. According to the Soderberg principle, the area of cross-section in mm2 of the bar for a factor of safety of 2 is
-
View Hint View Answer Discuss in Forum
Soderberg criteria is:
σa + σm σe σy+ = 1 and σa = 100 - 20 n 2A ⇒ 40 + 60 160 240 = 1 × A × 103 σm = 100 + 20 2 2A
A = 1000 mm2Correct Option: D
Soderberg criteria is:
σa + σm σe σy+ = 1 and σa = 100 - 20 n 2A ⇒ 40 + 60 160 240 = 1 × A × 103 σm = 100 + 20 2 2A
A = 1000 mm2
- A forged steel link with uniform diameter of 30 mm at the centre is subjected to an axial force that varies from 40 kN in compression to 160 kN in tension. The tensile (Su), yield (Sy) and corrected endurance (Se) strengths of the steel material are 600 MPa, 420 MPa and 240 MPa respectively. The factor of safety against fatigue endurance as per Soderberg's criterion is
-
View Hint View Answer Discuss in Forum
Fatigue endurance, σen = 240 MPa
A = π/4 × (30)2 × 706.5 × 10–6 m2
Soderberg’s equation is1 = σm + σa h σy σen.f Now Fm = 160 + 40 = 100 kN 2 ∴ σm = Fm = 100 kN = 141.54 MPa A 706.5 × 10 -6 and Fa = 160 - 40 = 60 kN 2 ∴ σa = 160 - 40 = 84.93 MPa 60 × 10 3 ∴ 1 = 141.54 + 84.93 h 420 240
or h = 1.45Correct Option: C
Fatigue endurance, σen = 240 MPa
A = π/4 × (30)2 × 706.5 × 10–6 m2
Soderberg’s equation is1 = σm + σa h σy σen.f Now Fm = 160 + 40 = 100 kN 2 ∴ σm = Fm = 100 kN = 141.54 MPa A 706.5 × 10 -6 and Fa = 160 - 40 = 60 kN 2 ∴ σa = 160 - 40 = 84.93 MPa 60 × 10 3 ∴ 1 = 141.54 + 84.93 h 420 240
or h = 1.45
- The forces F1 and F2 in a brake band and the direction of rotation of the drum are as shown in the figure. The coefficient of friction is 0.25. The angle of wrap is 3π/2 radians. It is given that R = 1 m and F2 = 1 N. The torque (in Nm) exerted on the drum is ________ .
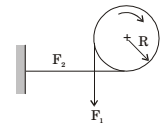
-
View Hint View Answer Discuss in Forum
F1 = e μ θ = e 0.25 × (3π / 2) = 3.248 F2
∴ F1 = 3.248 N
Torque, T = (F1 – F2) × r
= (3.248 – 1) × 1 = 2.248 N-mCorrect Option: C
F1 = e μ θ = e 0.25 × (3π / 2) = 3.248 F2
∴ F1 = 3.248 N
Torque, T = (F1 – F2) × r
= (3.248 – 1) × 1 = 2.248 N-m
- A four-wheel vehicle of mass 1000 kg moves uniformly in a straight line with the wheels revolving at 10 rad/s. The wheels are identical, each with a radius of 0.2 m. Then a constant braking torque is applied to all the wheels and the vehicle experience a uniform deceleration. For the vehicle to stop in 10s, the braking torque (in Nm) on each wheel is _______.
-
View Hint View Answer Discuss in Forum
m = 1000 kg, ω = 10 Rad/sec, R = 0.2 m, t = 10 sec
when ω = 0
∴ ωF = ωi – αt
∴ 0 = 10 – α .10
∴ α = 1 rad/ sec2
Now T = I.α∴ (T)each wheel = 
1000 
× 0.22 × 1 4
∴ (T)each wheel = 10 N - mCorrect Option: C
m = 1000 kg, ω = 10 Rad/sec, R = 0.2 m, t = 10 sec
when ω = 0
∴ ωF = ωi – αt
∴ 0 = 10 – α .10
∴ α = 1 rad/ sec2
Now T = I.α∴ (T)each wheel = 
1000 
× 0.22 × 1 4
∴ (T)each wheel = 10 N - m
- A drum brake is shown in the figure. The drum is rotating in anticlockwise direction. The coefficient of friction between drum and shoe is 0.2. The dimensions shown in the figure are in mm. The braking torque (in Nm) for the brake shoe is________.
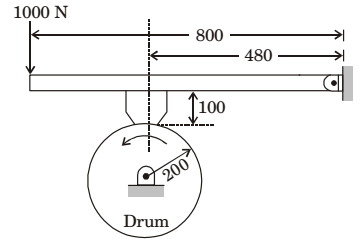
-
View Hint View Answer Discuss in Forum
Taking moments about pin joint (SM)
⇒ 1000 × 0.8 =RN × 0.48 + μRN × 0.1⇒ RN = 800 = 1600 0.5
TB = μRN × r= 0.2 × 1600 × 200 = 64 N - M 1000 Correct Option: A
Taking moments about pin joint (SM)
⇒ 1000 × 0.8 =RN × 0.48 + μRN × 0.1⇒ RN = 800 = 1600 0.5
TB = μRN × r= 0.2 × 1600 × 200 = 64 N - M 1000

