Engineering Mechanics Miscellaneous

Engineering Mechanics Miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Engineering Mechanics

Engineering Mechanics Miscellaneous
  1. A block R of mass 100 kg is placed on a block S of mass 150 kg as shown in the figure. Block R is tied to the wall by a mass less and in extensible string PQ. If the coefficient of static friction for all surfaces is 0.4, the minimum force F(in kN) needed to move the block S is








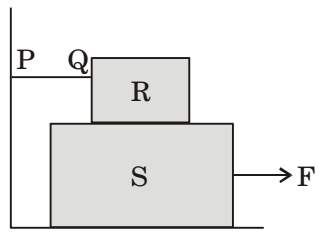
  1. View Hint View Answer Discuss in Forum


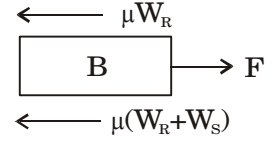
    F = μ (Ws + WR) + μ WR
    F = μ (Ws + 2WR)
    = 0.4 (150 + 2 × 1000)9.81 = 1.37 kN

    Correct Option: D


    F = μ (Ws + WR) + μ WR
    F = μ (Ws + 2WR)
    = 0.4 (150 + 2 × 1000)9.81 = 1.37 kN

  1. A1 kg block is resting on a surface with coefficient of friction μ = 0.1. A force of 0.8 N is applied to the block as shown in the figure. The friction force is








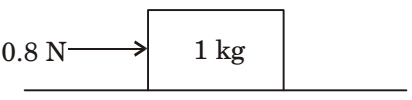
  1. View Hint View Answer Discuss in Forum

    Limiting friction force between block and the surface is 0.98 N. But applied force is 0.8 N which is less than the limiting friction force. Therefore friction force for the given case is 0.8 N.

    Correct Option: B

    Limiting friction force between block and the surface is 0.98 N. But applied force is 0.8 N which is less than the limiting friction force. Therefore friction force for the given case is 0.8 N.

  1. A block weighing 981 N is resting on a horizontal surface. The coefficient of friction between the block and the horizontal surface is μ = 0.2. A vertical cable attached to the block provides partial support as shown. A man can pull horizontally with a force of 100 N. What will be the tension, T (in N) in the cable if the man is just able to move the block to the right?








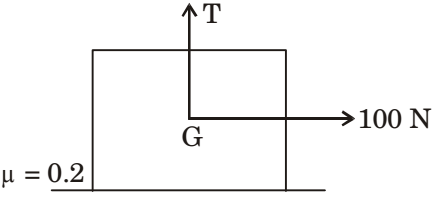
  1. View Hint View Answer Discuss in Forum

    Net normal force on block
    N = W – T
    = 981 – T
    Frictional force,f = μN
    Under equilibrium, i.e. when man is just able to move the block
    μN = 100
    ⇒ μ(981–T) = 100
    ⇒ 0.2 (981 – T) = 100

    T = -
    100
    		+ 981
    0.2

    = 981 – 500 = 481N

    Correct Option: C

    Net normal force on block
    N = W – T
    = 981 – T
    Frictional force,f = μN
    Under equilibrium, i.e. when man is just able to move the block
    μN = 100
    ⇒ μ(981–T) = 100
    ⇒ 0.2 (981 – T) = 100

    T = -
    100
    		+ 981
    0.2

    = 981 – 500 = 481N

  1. A block of mass M is released from point P on a rough inclined plane with inclination angle θ, shown in the figure below. The coefficient of friction is μ. If μ < tan θ, then the time taken by the block to reach another point Q on the inclined plane, where PQ = s, is








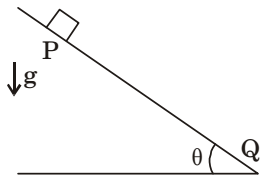
  1. View Hint View Answer Discuss in Forum


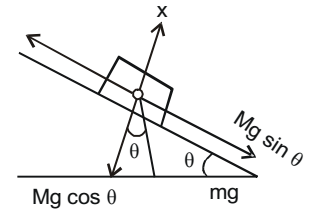
    Mg sin θ – μ Mg cos θ= Ma
    ⇒ a = g sin θ – μ g cos θ

    Now s = ut +
    1
    		at2
    2

    But u = 0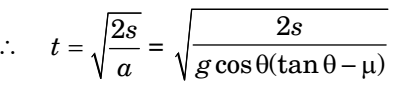

    Correct Option: A


    Mg sin θ – μ Mg cos θ= Ma
    ⇒ a = g sin θ – μ g cos θ

    Now s = ut +
    1
    		at2
    2

    But u = 0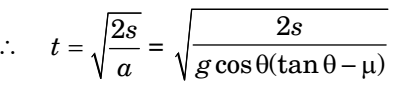

  1. Two books of mass 1 kg each are kept on a table, one over the other. The coefficient of friction on every pair of contacting surfaces is 0.3. The lower book is pulled with a horizontal force F. The minimum value of F for which slip occurs between the two books is








  1. View Hint View Answer Discuss in Forum

    [amax]A = ?
    [amax]A → [(fs)max]AB
    A → 3N
    [(fx)max]AB = μsNAB
    = 0.3 × 9.81 = 2.943 N

    (aA)max =
    [(fs)max]AB
    		= 2.943 m/s2
    mA

    At that condition,

    Fmin – 8.829 = mB aB
    Fmin = 8.829 + 1 × 2.943
    Fmin = 11.772 N

    Correct Option: B

    [amax]A = ?
    [amax]A → [(fs)max]AB
    A → 3N
    [(fx)max]AB = μsNAB
    = 0.3 × 9.81 = 2.943 N

    (aA)max =
    [(fs)max]AB
    		= 2.943 m/s2
    mA

    At that condition,

    Fmin – 8.829 = mB aB
    Fmin = 8.829 + 1 × 2.943
    Fmin = 11.772 N