6. A two member truss PQR is supporting a load W. The axial forces in members PQ and QR are respectively
   
   

1. 1. 2W tensile and √3W compressive
      

   
   
   

   2. √3W tensile and 2W compressive
      

   
   
   

   3. √3W compressive and 2W tensile
      

   
   
   

   4. 2W compressive and √3W tensile

   
   
   

---

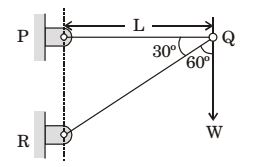
1. View Hint View Answer Discuss in Forum

   
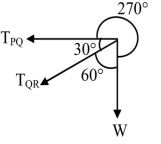
   Lami’s theorem is used to find the F
   

   	W	=	TPQ	=	TQR
   	sin 30°		sin 60°		sin 270°

   
   ⇒ T_PQ = √3W (T)
   ⇒ T_QR = – 2 W = 2W(C)

   Correct Option: C

   
   Lami’s theorem is used to find the F
   

   	W	=	TPQ	=	TQR
   	sin 30°		sin 60°		sin 270°

   
   ⇒ T_PQ = √3W (T)
   ⇒ T_QR = – 2 W = 2W(C)

---

7. A circular solid disc of uniform thickness 20 mm, radius 200 mm and mass 20 kg, is used as a flywheel. If it rotates at 600 rpm, the kinetic energy of the flywheel, in Joules is

1. 1. 395

   
   
   

   2. 790

   
   
   

   3. 1580

   
   
   

   4. 3160

   
   
   

---

1. View Hint View Answer Discuss in Forum

   K.E. of fly wheel =	1	ω2
   	2

   
   

   where, I =	mR2	=	20 × 0.22	= 0.4 kg- m2
   	2		2

   
   

   ω =	2πN	=	2 × π × 600	= 62.83 rad/s
   	60		60

   
   

   K.E.=	1	× 0.4 × 62.832 = 790 J
   	2

   Correct Option: B

   K.E. of fly wheel =	1	ω2
   	2

   
   

   where, I =	mR2	=	20 × 0.22	= 0.4 kg- m2
   	2		2

   
   

   ω =	2πN	=	2 × π × 600	= 62.83 rad/s
   	60		60

   
   

   K.E.=	1	× 0.4 × 62.832 = 790 J
   	2

---

---

8. Consider a fly wheel whose mass M is distributed almost equally between a heavy, ring-like rim of radius P and a concentric disk-like feature of radius R/2. Other parts of the flywheel, such as spokes, etc, have negligible mass. The best approximation for α, if the moment Of inertia of the flywheel about its axis of rotation is expressed as αMR₂, is _______.

1. 1. 0.56

   
   
   

   2. 0.51

   
   
   

   3. 0.55

   
   
   

   4. 0.59

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Moment of Inertia of fly wheel
   I = m_rR²
   R = mean Radius of Rim
   

   = M		R + R/2		2
   		2

   
   = 0.56 MR²
   ⇒ α = 0.56

   Correct Option: A

   Moment of Inertia of fly wheel
   I = m_rR²
   R = mean Radius of Rim
   

   = M		R + R/2		2
   		2

   
   = 0.56 MR²
   ⇒ α = 0.56

---

9. The position vector OP of point P(20, 10) is rotated anti-clockwise in X-Y plane by an angle θ = 30° a such that point P occupies position Q, as shown in the figure. The coordinates (x, y) of Q are
   

1. 1. (12.32, 18.66)

   
   
   

   2. (18.66, 12.32)

   
   
   

   3. (22.32 ,8.26)

   
   
   

   4. (13.40, 22.32)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Let Co-ordinates of Q are (x', y') and rotation about x-y plane anti clockwise.
   

   X'

   =

   cosθ

   -sinθ

   X

   Y'

   sinθ

   cosθ

   Y

   
   

   X'

   =

   cos30

   -sin30

   20

   Y'

   sin30

   cos30

   10

   
   

   =		0.866	-0.5				20
   		0.5	0.866				10

   
   

   X'

   =

   0.866 × 20

   -0.5 × 10

   =

   12.32

   Y'

   0.5 × 20

   0.866 × 10

   18.66

   
   (x', y') = (12.32, 18.66)

   Correct Option: A

   Let Co-ordinates of Q are (x', y') and rotation about x-y plane anti clockwise.
   

   X'

   =

   cosθ

   -sinθ

   X

   Y'

   sinθ

   cosθ

   Y

   
   

   X'

   =

   cos30

   -sin30

   20

   Y'

   sin30

   cos30

   10

   
   

   =		0.866	-0.5				20
   		0.5	0.866				10

   
   

   X'

   =

   0.866 × 20

   -0.5 × 10

   =

   12.32

   Y'

   0.5 × 20

   0.866 × 10

   18.66

   
   (x', y') = (12.32, 18.66)

---

---

10. The rod PQ of length L = 2 m and uniformly distributed mass of M = 10 kg, is released from rest at the position shown in the figure. The ends slide along the friction less faces OP and OQ. Assume acceleration due to gravity, g = 10 m/s². The mass moment of inertia of the rod about its centre of mass and an axis perpendicular to the plane of the figure is (ML²/12). At this instant, the magnitude of angular acceleration (in radian/s²) of the rod is ______.'
    

1. 1. 7.5

   
   
   

   2. 7.8

   
   
   

   3. 7.7

   
   
   

   4. 7.6

   
   
   

---

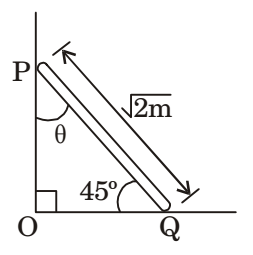
1. View Hint View Answer Discuss in Forum

   
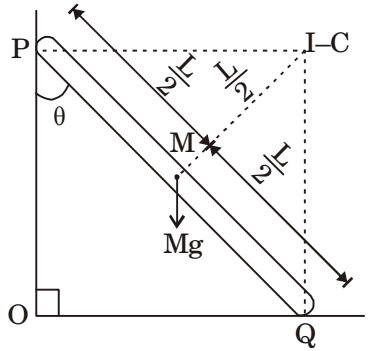
   T_I-C = T_I-C
   

   ⇒ Mgx	L	cos45° =		ICM +	ML2		α
   	2				4

   
   

   ⇒ Mg	L	cos45° =		ML2	+	ML2		α
   	2			12		4

   
   

   α =	3g	cos45°
   	2L

   
   

   α =	30	+	1		∴ g = 10	m
   	2 × V2		V2			s2

   
   

   α = 7.5	rad
   	s2

   Correct Option: A

   
   T_I-C = T_I-C
   

   ⇒ Mgx	L	cos45° =		ICM +	ML2		α
   	2				4

   
   

   ⇒ Mg	L	cos45° =		ML2	+	ML2		α
   	2			12		4

   
   

   α =	3g	cos45°
   	2L

   
   

   α =	30	+	1		∴ g = 10	m
   	2 × V2		V2			s2

   
   

   α = 7.5	rad
   	s2

---