-
The rod PQ of length L = 2 m and uniformly distributed mass of M = 10 kg, is released from rest at the position shown in the figure. The ends slide along the friction less faces OP and OQ. Assume acceleration due to gravity, g = 10 m/s2. The mass moment of inertia of the rod about its centre of mass and an axis perpendicular to the plane of the figure is (ML2/12). At this instant, the magnitude of angular acceleration (in radian/s2) of the rod is ______.'
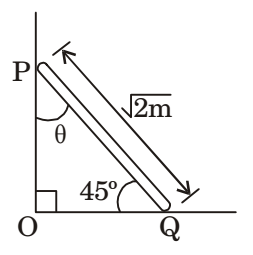
-
- 7.5
- 7.8
- 7.7
- 7.6
Correct Option: A
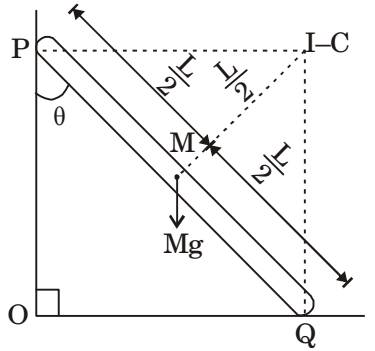
TI-C = TI-C
| ⇒ Mgx | cos45° = |  | ICM + |  | α | ||
| 2 | 4 |
| ⇒ Mg | cos45° = |  | + |  | α | |||
| 2 | 12 | 4 |
| α = | cos45° | 2L |
| α = | + |  | ∴ g = 10 |  | |||
| 2 × V2 | V2 | s2 |
| α = 7.5 | s2 |

