11. The position vector OP of point P(20, 10) is rotated anti-clockwise in X-Y plane by an angle θ = 30° a such that point P occupies position Q, as shown in the figure. The coordinates (x, y) of Q are
    

1. 1. (12.32, 18.66)

   
   
   

   2. (18.66, 12.32)

   
   
   

   3. (22.32 ,8.26)

   
   
   

   4. (13.40, 22.32)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Let Co-ordinates of Q are (x', y') and rotation about x-y plane anti clockwise.
   

   X'

   =

   cosθ

   -sinθ

   X

   Y'

   sinθ

   cosθ

   Y

   
   

   X'

   =

   cos30

   -sin30

   20

   Y'

   sin30

   cos30

   10

   
   

   =		0.866	-0.5				20
   		0.5	0.866				10

   
   

   X'

   =

   0.866 × 20

   -0.5 × 10

   =

   12.32

   Y'

   0.5 × 20

   0.866 × 10

   18.66

   
   (x', y') = (12.32, 18.66)

   Correct Option: A

   Let Co-ordinates of Q are (x', y') and rotation about x-y plane anti clockwise.
   

   X'

   =

   cosθ

   -sinθ

   X

   Y'

   sinθ

   cosθ

   Y

   
   

   X'

   =

   cos30

   -sin30

   20

   Y'

   sin30

   cos30

   10

   
   

   =		0.866	-0.5				20
   		0.5	0.866				10

   
   

   X'

   =

   0.866 × 20

   -0.5 × 10

   =

   12.32

   Y'

   0.5 × 20

   0.866 × 10

   18.66

   
   (x', y') = (12.32, 18.66)

---

12. The rod PQ of length L = 2 m and uniformly distributed mass of M = 10 kg, is released from rest at the position shown in the figure. The ends slide along the friction less faces OP and OQ. Assume acceleration due to gravity, g = 10 m/s². The mass moment of inertia of the rod about its centre of mass and an axis perpendicular to the plane of the figure is (ML²/12). At this instant, the magnitude of angular acceleration (in radian/s²) of the rod is ______.'
    

1. 1. 7.5

   
   
   

   2. 7.8

   
   
   

   3. 7.7

   
   
   

   4. 7.6

   
   
   

---

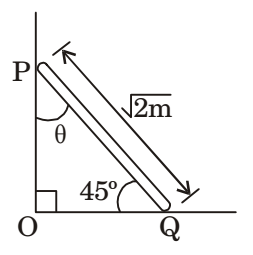
1. View Hint View Answer Discuss in Forum

   
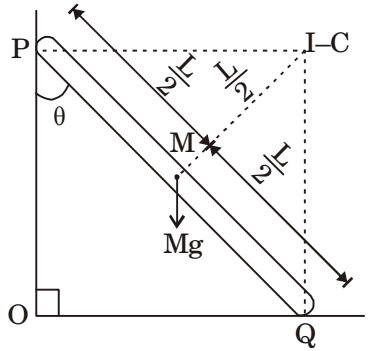
   T_I-C = T_I-C
   

   ⇒ Mgx	L	cos45° =		ICM +	ML2		α
   	2				4

   
   

   ⇒ Mg	L	cos45° =		ML2	+	ML2		α
   	2			12		4

   
   

   α =	3g	cos45°
   	2L

   
   

   α =	30	+	1		∴ g = 10	m
   	2 × V2		V2			s2

   
   

   α = 7.5	rad
   	s2

   Correct Option: A

   
   T_I-C = T_I-C
   

   ⇒ Mgx	L	cos45° =		ICM +	ML2		α
   	2				4

   
   

   ⇒ Mg	L	cos45° =		ML2	+	ML2		α
   	2			12		4

   
   

   α =	3g	cos45°
   	2L

   
   

   α =	30	+	1		∴ g = 10	m
   	2 × V2		V2			s2

   
   

   α = 7.5	rad
   	s2

---

---

13. A mobile phone has a small motor with an eccentric mass used for vibrator mode. The location of the eccentric mass on motor with respect to center of gravity (CG) of the mobile and the rest of the dimension of the mobile phone are shown. The mobile is kept on a flat horizontal surface.
    
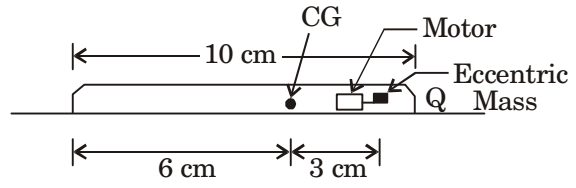
    Given in addition that the eccentric mass = 2 grams, eccentricity = 2.19 mm, mass of the mobile = 90 grams, g= 9.81 m/s². Uniform speed of the motor in RPM for which the mobile will get just lifted off the ground at the end Q is approximately

1. 1. 3000

   
   
   

   2. 3500

   
   
   

   3. 4000

   
   
   

   4. 4500

   
   
   

---

1. View Hint View Answer Discuss in Forum

   When lifted from ground at Q
   Reaction = 0
   ∴ taking moments about ‘p’ and equating to 0
   .09 × .06 = mr ω² × .09
   9.01 × .09 × .06 = .002 × 2.19 × 10^-3 × ω² × .09
   ⇒ ω = 366.50 rad/s
   = 3500 rpm

   Correct Option: B

   When lifted from ground at Q
   Reaction = 0
   ∴ taking moments about ‘p’ and equating to 0
   .09 × .06 = mr ω² × .09
   9.01 × .09 × .06 = .002 × 2.19 × 10^-3 × ω² × .09
   ⇒ ω = 366.50 rad/s
   = 3500 rpm

---

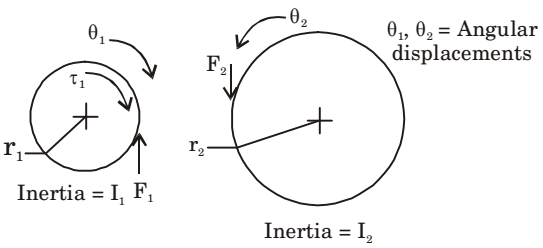
14. A pinion with radius r₁, and inertia I₁, is driving a gear with radius r₂ and inertia I₂. Torque τ₁ is applied on pinion. The following are free body diagrams of pinion and gear showing important forces (F₁ and F₂) of interaction. Which of the following relations hold true?
    

1. 1. 

   
   
   

   2. 

   
   
   

   3. 

   
   
   

   4. 

   
   
   

---

1. View Hint View Answer Discuss in Forum

   F₁ = F₂ [Vertical equilibrium]
   For Gear 1, For Gear 2,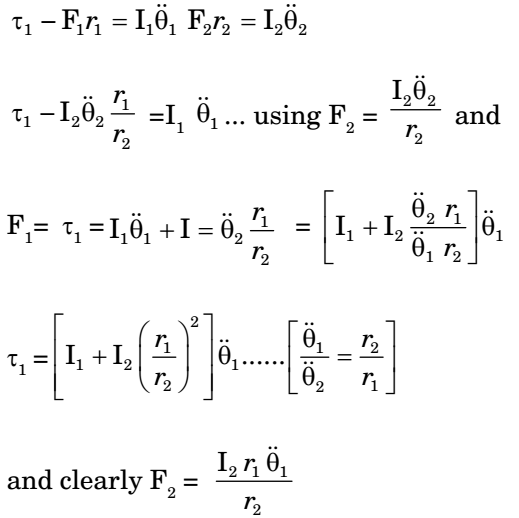
   

   Correct Option: B

   F₁ = F₂ [Vertical equilibrium]
   For Gear 1, For Gear 2,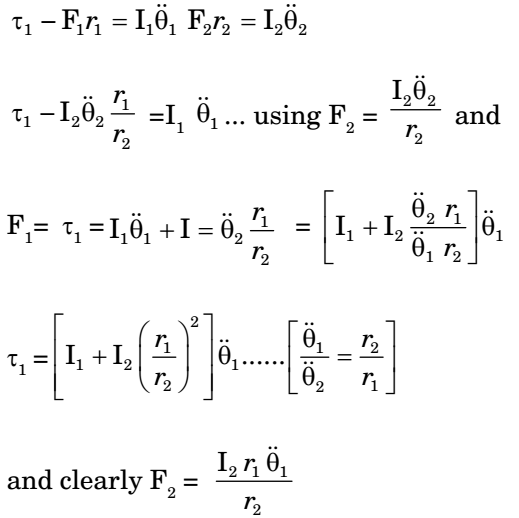
   

---

---

15. A two member truss ABC is shown in the figure. The force (in kN) transmitted in member AB is ______
    

1. 1. 20 kN

   
   
   

   2. 10 kN

   
   
   

   3. 40 kN

   
   
   

   4. None of these

   
   
   

---

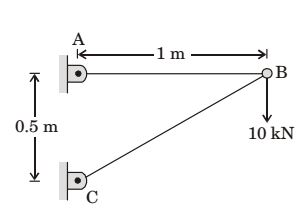
1. View Hint View Answer Discuss in Forum

   
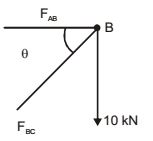
   FBD of joint B
   

   θ = tan-1		0.5		= 26.5
   		1

   
   ∑V = 0
   

   	FBC sinθ	=	10 kN
   	FBC cosθ		FAB

   
   

   FAB =	10	= 20 kN
   	tan(26.2)

   Correct Option: A

   
   FBD of joint B
   

   θ = tan-1		0.5		= 26.5
   		1

   
   ∑V = 0
   

   	FBC sinθ	=	10 kN
   	FBC cosθ		FAB

   
   

   FAB =	10	= 20 kN
   	tan(26.2)

---