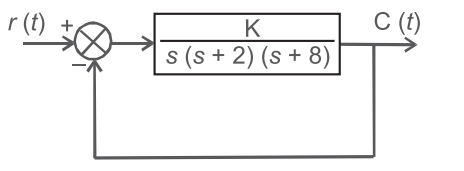
36. By a suitable choice of the scalar parameter K, the system shown in the figure below, can be made to oscillate continuously at a frequency of—
    
    
    
    

1. 1. 1 rad/s
      

   
   
   

   2. 2 rad/s
      

   
   
   

   3. 4 rad/s
      

   
   
   

   4. 8 rad/s

   
   
   

---

1. View Hint View Answer Discuss in Forum

   To make the system oscillatory the imaginary part in the C.E. equation of the given system must be zero. So first we calculate C.E.
   Here,
   

   G(s)	K
   	s(s + 2) (s + 8)

   
   H(s) = 1
   1 + G(s) H(s) = 0 is the C.E.
   or s
   (s + 2) (s + 8) + K = 0
   s (s² + 10s + 16) + K = 0 (∴ s = jω)
   jω(– ω² + 10 jω + 16) + K = 0
   – jω³ – 10ω² + K = 0
   – j(ω³ – 16ω) – 10ω² + K = 0
   Hence for system to be oscillatory
   ω³ – 16ω = 0
   ω² – 16 = 0
   or
   ω = 4

   
   

   Correct Option: C

   To make the system oscillatory the imaginary part in the C.E. equation of the given system must be zero. So first we calculate C.E.
   Here,
   

   G(s)	K
   	s(s + 2) (s + 8)

   
   H(s) = 1
   1 + G(s) H(s) = 0 is the C.E.
   or s
   (s + 2) (s + 8) + K = 0
   s (s² + 10s + 16) + K = 0 (∴ s = jω)
   jω(– ω² + 10 jω + 16) + K = 0
   – jω³ – 10ω² + K = 0
   – j(ω³ – 16ω) – 10ω² + K = 0
   Hence for system to be oscillatory
   ω³ – 16ω = 0
   ω² – 16 = 0
   or
   ω = 4

   
   

---

37. The open-loop transfer function with unity feedback are given below for different systems
    

    1. G(s) =	2
    	s + 2

    
    

    2. G(s) =	2
    	s(s + 2)

    
    

    3. G(s) =	2
    	s2(s + 2)

    
    

    4. G(s) =	2(s + 1)
    	s(s + 2)

    
    Among these systems, the unstable system is—
    

1. 1. 1
      

   
   
   

   2. 2
      

   
   
   

   3. 3
      

   
   
   

   4. 4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   In order to check the stability of the system, apply R.H.C.
   Given
   H(s) = 1
   For 1st system
   

   G(s) =	2
   	(s + 2)

   
   

   C.E. = 1 + G(s) H(s) = 1 +	2	1 = s + 4 = 0 stable
   	s + 2

   
   For 2nd system
   

   G(s) = 1	2
   	s(s + 2)

   
   C.E. = 1 + G(s) H(s) = 0
   

   = 1 +	2	. 1 = s2 + 2s + 2 = 0
   	s(s + 2)

   
   s² 1 2
   s₁ 2 0
   s₀ 3
   Hence system is stable.
   for 3rd system
   

   G(s) =	2
   	s2(s + 2)

   
   C.E. = 1 + G(s) H(s) = 0
   

   1 +	1	. 1 = s3 + 2s2 + 2 = 0
   	s(s + 2)

   
   From this expression we see that there is one missing form (i.e., s).
   Hence the system is unstable.

   Correct Option: C

   In order to check the stability of the system, apply R.H.C.
   Given
   H(s) = 1
   For 1st system
   

   G(s) =	2
   	(s + 2)

   
   

   C.E. = 1 + G(s) H(s) = 1 +	2	1 = s + 4 = 0 stable
   	s + 2

   
   For 2nd system
   

   G(s) = 1	2
   	s(s + 2)

   
   C.E. = 1 + G(s) H(s) = 0
   

   = 1 +	2	. 1 = s2 + 2s + 2 = 0
   	s(s + 2)

   
   s² 1 2
   s₁ 2 0
   s₀ 3
   Hence system is stable.
   for 3rd system
   

   G(s) =	2
   	s2(s + 2)

   
   C.E. = 1 + G(s) H(s) = 0
   

   1 +	1	. 1 = s3 + 2s2 + 2 = 0
   	s(s + 2)

   
   From this expression we see that there is one missing form (i.e., s).
   Hence the system is unstable.

---

---

38. Consider the following statements with reference to phase lead compensator.
    1. increases the margin of stability
    2. speeds up transient response
    3. does not affect the system error constant. Of these statements—
    

1. 1. 2 and 3 are correct
      

   
   
   

   2. 1 and 2 are correct
      

   
   
   

   3. 1 and 3 are correct
      

   
   
   

   4. 1, 2 and 3 are correct

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Lead compensator
   ● Increases the margin of stability.
   ● It also speed up transient response.

   Correct Option: B

   Lead compensator
   ● Increases the margin of stability.
   ● It also speed up transient response.

---

39. For a feedback control system of type 2, the steady state error for a ramp input is—
    

1. 1. infinite
      

   
   
   

   2. constant
      

   
   
   

   3. zero
      

   
   
   

   4. indeterminate

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Refer synopsis.

   Correct Option: C

   Refer synopsis.

---

---

40. The performance specifications for a unity feedback control system having an open-loop transfer function
    

    G(s) =	K	are
    	s(s + 1)(s + 2)

    
    (i) Velocity error coefficient KV > 10 sec^–1
    (ii) Stable closed-loop operation. The value of K, satisfying the above specifications, is—
    

1. 1. K > 6
      

   
   
   

   2. 6 < K < 10
      

   
   
   

   3. K > 10
      

   
   
   

   4. K > 20

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Since,
   KV = _{s → 0}Lim sG(s)
   or
   

   KV = s → 0Lim	s × K	=	K
   	s(s + 1)(s + 2)		2

   
   but given
   KV > 10
   then
   K > 20

   Correct Option: D

   Since,
   KV = _{s → 0}Lim sG(s)
   or
   

   KV = s → 0Lim	s × K	=	K
   	s(s + 1)(s + 2)		2

   
   but given
   KV > 10
   then
   K > 20

---