Control systems miscellaneous

Control systems miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Control Systems

Control systems miscellaneous
  1. The transfer function of a system is
    2s2 + 6s + 5
    (s + 1)2(s + 2)

    The characteristic equation of the system is—








  1. View Hint View Answer Discuss in Forum

    The given T.F. is

    C(s)
    		 =
    G(s)
    		 =
    2s2 + 6s + 5
    R(s)1 + G(s) H(s)(s + 1)2 (s + 2)

    C.E. = 1 + G(s) H(s) = (s + 1)2 (s + 2)

    Correct Option: B

    The given T.F. is

    C(s)
    		 =
    G(s)
    		 =
    2s2 + 6s + 5
    R(s)1 + G(s) H(s)(s + 1)2 (s + 2)

    C.E. = 1 + G(s) H(s) = (s + 1)2 (s + 2)

  1. A system is represented by
    dy
    		+ 2y = 4t u(t)
    dt

    The ramp component in the forced response will be—








  1. View Hint View Answer Discuss in Forum

    Given equation

    dy
    		+ 2y = 4t u(t)
    dt

    taking Laplace transform of the given equation
    sY(s) + 2Y(s) = 4/s2
    or
    Y (s) [s + 2] = 4/s2
    or
    Y(s) = 4/s2(s + 2)
    or
    Y(s) = – (1/s) + (2/s2) + 1/(s + 2)
    y(t) = – u(t) + 2tu(t) + e–2t
    Here the ramp component in the forced response is 2tu(t). Hence alternative (B) is the correct choice.

    Correct Option: B

    Given equation

    dy
    		+ 2y = 4t u(t)
    dt

    taking Laplace transform of the given equation
    sY(s) + 2Y(s) = 4/s2
    or
    Y (s) [s + 2] = 4/s2
    or
    Y(s) = 4/s2(s + 2)
    or
    Y(s) = – (1/s) + (2/s2) + 1/(s + 2)
    y(t) = – u(t) + 2tu(t) + e–2t
    Here the ramp component in the forced response is 2tu(t). Hence alternative (B) is the correct choice.

  1. The Nyquist locus of a transfer function
    G(s) H(s) =
    K
    1 + sT1

    in given below in figure The locus is modified as shown below in figure, on addition of poles to the original G (s) H (s). Then, the transfer function of the modified locus is—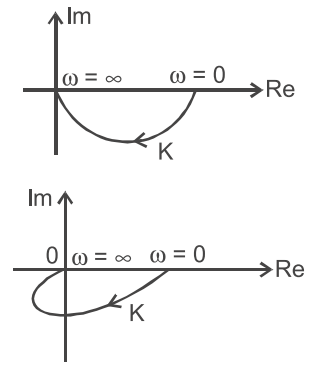










  1. View Hint View Answer Discuss in Forum

    From the given Nyquist plot we conclude that both the Nyquist plot have phase = 0° at ω = 0.
    and it can be possible only from the modified transfer function given in option (B) only.
    Hence alternative (B) is the correct choice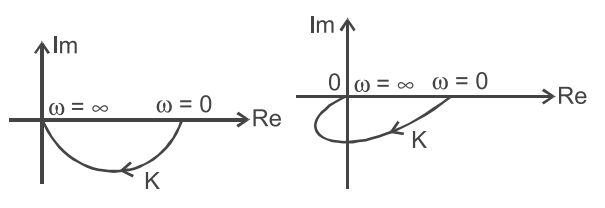


    Correct Option: B

    From the given Nyquist plot we conclude that both the Nyquist plot have phase = 0° at ω = 0.
    and it can be possible only from the modified transfer function given in option (B) only.
    Hence alternative (B) is the correct choice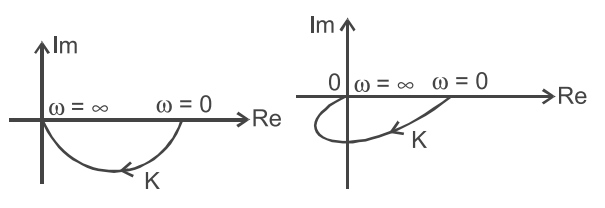


  1. The transfer function of a compensating network is of the form
    1 + αTs
    1 + Ts

    If this is a phase-lag network, the value of α should be—








  1. View Hint View Answer Discuss in Forum

    Refer synopsis.

    Correct Option: B

    Refer synopsis.

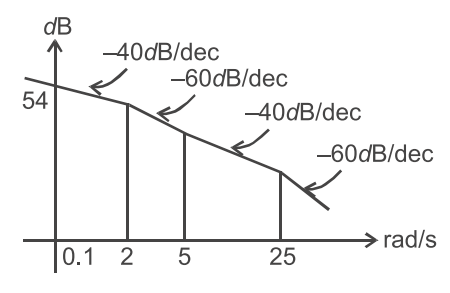
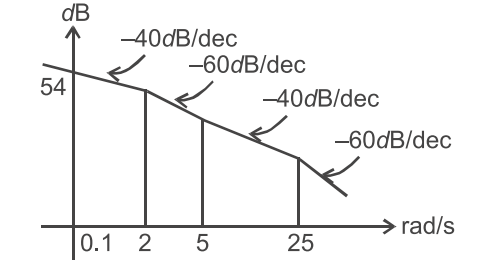
  1. The asymptotic approximation of the log-magnitude versus frequency plot of a minimum phase system with real poles and one zero is shown in figure. Its transfer function is—










  1. View Hint View Answer Discuss in Forum

    From figure we conclude at ω = 0·1.
    Slope is – 40 dB/dec, it means there are two poles at the origin.
    at ω = 2 gain is decay from – 40 dB/dec to – 60 dB/dec it means there is another pole at s = –2 or (s + 2).
    and at ω = 5 gain is increases from – 60 dB/dec to – 40 dB/dec, it means there is zero at s = – 5 or (s + 5) and finally another pole at s = –25 or (s + 25). so, the transfer function of the form

    G(s) =
    K(s + 5)
    s2(s + 2)(s + 25)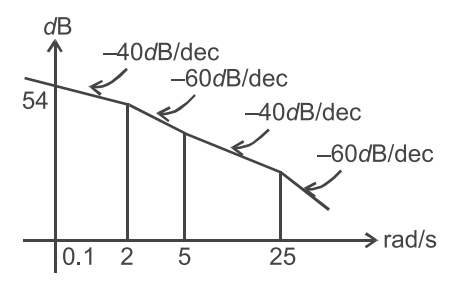


    Correct Option: D

    From figure we conclude at ω = 0·1.
    Slope is – 40 dB/dec, it means there are two poles at the origin.
    at ω = 2 gain is decay from – 40 dB/dec to – 60 dB/dec it means there is another pole at s = –2 or (s + 2).
    and at ω = 5 gain is increases from – 60 dB/dec to – 40 dB/dec, it means there is zero at s = – 5 or (s + 5) and finally another pole at s = –25 or (s + 25). so, the transfer function of the form

    G(s) =
    K(s + 5)
    s2(s + 2)(s + 25)