Boats and Streams
- A boat goes 6 km an hour in still water, but takes thrice as much time in going the same distance against the current. The speed of the current (in km/hour) is :
-
View Hint View Answer Discuss in Forum
Let the speed of the current be y kmph.
∴ speed of boat = 6 kmph.
According to the question,6 = 3 6 - y
⇒ 18 – 3y = 6
⇒ 3y = 18 – 6 ⇒ 3y = 12⇒ y = 12 = 4kmph 3
We can find the required answer with the help of given formula :
Here, Speed of boat = 6 km/hr
t1 = 3k, t2 = kSpeed of Boat = t1 + t2 Speed of Stream t1 - t2
Correct Option: A
Let the speed of the current be y kmph.
∴ speed of boat = 6 kmph.
According to the question,6 = 3 6 - y
⇒ 18 – 3y = 6
⇒ 3y = 18 – 6 ⇒ 3y = 12⇒ y = 12 = 4kmph 3
We can find the required answer with the help of given formula :
Here, Speed of boat = 6 km/hr
t1 = 3k, t2 = kSpeed of Boat = t1 + t2 Speed of Stream t1 - t2 6 = 3k + k Speed of Stream 3k - k
Speed of current = 3 km/hr
- A man can row 30 km downstream and return in a total of 8 hours. If the speed of the boat in still water is four times the speed of the current, then the speed of the current is
-
View Hint View Answer Discuss in Forum
Let the speed of stream be k kmph, then speed of boat in still water = 4k kmph
∴ Rate downstream = 4k + k = 5k kmph
Rate upstream = 4k – k = 3k kmph
From the question ,⇒ 30 + 30 = 8 ⇒ 10 + 6 = 8 3k 5k k k
Correct Option: B
Let the speed of stream be k kmph, then speed of boat in still water = 4k kmph
∴ Rate downstream = 4k + k = 5k kmph
Rate upstream = 4k – k = 3k kmph
From the question ,⇒ 30 + 30 = 8 ⇒ 10 + 6 = 8 3k 5k k k ⇒ 16 = 8 ⇒ k = 16 = 2 kmph k 8
-
A person can row 7 1 km an hour in still water and he finds 2
that it takes him twice as long to row up as to row down the river. The speed of the stream is :
-
View Hint View Answer Discuss in Forum
Let the speed of current be y kmph.
According to question ,∴ 2 
15 - y 
= 15 + y 2 2 ⇒ 15 - 2y = 15 + y 2 ⇒ 3y = 15 - 15 = 15 2 2 ⇒ y = 5 = 2 1 kmph 2 2
We can find the required answer with the help of given formula :Here, Speed of Boat = 15 kmph 2
t1 = 2k, t2 = kSpeed of Boat = t1 + t2 Speed of Stream t1 - t2
Correct Option: C
Let the speed of current be y kmph.
According to question ,∴ 2 
15 - y 
= 15 + y 2 2 ⇒ 15 - 2y = 15 + y 2 ⇒ 3y = 15 - 15 = 15 2 2 ⇒ y = 5 = 2 1 kmph 2 2
We can find the required answer with the help of given formula :Here, Speed of Boat = 15 kmph 2
t1 = 2k, t2 = kSpeed of Boat = t1 + t2 Speed of Stream t1 - t2 
15 
= 2k + k 2 × Speed of Stream 2k - k
Speed of Stream = 2.5 km/hr
-
as long to row a distance upstream as to row the same distance downstream, then, the speed of stream (in km/hr) isA man can row at a speed of 4 1 km/hr in still water. If he takes 2 times 2
-
View Hint View Answer Discuss in Forum
Let the speed of stream be x kmph
∴ Rate upstream = 9 - x 2 Rate downstream = 9 + x 2
Then, According to question ,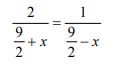
⇒ 9 - 2x = 9 + x 2 ⇒ 3x = 9 - 9 = 9 2 2 ⇒ x = 9 = 3 = 1.5 kmph 2 × 3 2
Using the given formula :
Here, t1 = 2k , t2 = kSpeed of Boat = 9 kmph 2
Correct Option: B
Let the speed of stream be x kmph
∴ Rate upstream = 9 - x 2 Rate downstream = 9 + x 2
Then, According to question ,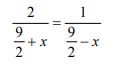
⇒ 9 - 2x = 9 + x 2 ⇒ 3x = 9 - 9 = 9 2 2 ⇒ x = 9 = 3 = 1.5 kmph 2 × 3 2
Using the given formula :
Here, t1 = 2k , t2 = kSpeed of Boat = 9 kmph 2 Speed of Boat = t1 + t2 Speed of Stream t1 - t2 9 = 2k + k 2 × Speed of Stream 2k - k
Speed of Stream = 1.5 km/hr
- A boat can travel with a speed of 13 km/hr in still water. If the speed of stream is 4 km/hr in the same direction, time taken by boat to go 63 km in opposite direction is
-
View Hint View Answer Discuss in Forum
Given that , speed of stream = 4 km/h
speed of boat = 13 km/h
Rate upstream of boat = 13 – 4 = 9 kmph
Distance = 63 km∴ Required time = Distance Speed ∴ Required time = 63 = 7 hours 9
Correct Option: B
Given that , speed of stream = 4 km/h
speed of boat = 13 km/h
Rate upstream of boat = 13 – 4 = 9 kmph
Distance = 63 km∴ Required time = Distance Speed ∴ Required time = 63 = 7 hours 9
We can find the required answer with the help of given formula :∴ Speed = Distance Time

