Materials Science and Manufacturing Engineering Miscellaneous

Materials Science and Manufacturing Engineering Miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Materials Science and Manufacturing Engineering

Materials Science and Manufacturing Engineering Miscellaneous
  1. Match the Machine Tools (Group A) with the probable Operations (Group B) :
    Group A Group B
    P. Centre Lathe1. Slotting
    Q. Milling2. Counter-boring
    R. Grinding3. Knurling
    S. Drilling4. Dressing









  1. View Hint View Answer Discuss in Forum

    Centre lathe - knurling Milling – Slotting Grinding – Dressing Drilling – Center Boring

    Correct Option: C

    Centre lathe - knurling Milling – Slotting Grinding – Dressing Drilling – Center Boring

  1. The main cutting force acting on a tool during the turning (orthogonal cutting) operation of a metal is 400 N. The turning was performed using 2 mm depth of cut and 0.1 mm/rev feed rate. The specific cutting pressure (in N/mm2) is








  1. View Hint View Answer Discuss in Forum

    ∴ Specific cutting pressure =
    Fc
    		 =
    400
    		 = 2000 N / mm2
    W.t2 × 0.1

    Correct Option: B

    ∴ Specific cutting pressure =
    Fc
    		 =
    400
    		 = 2000 N / mm2
    W.t2 × 0.1

Direction: In Orthogonal turning of a bar of 100 mm diameter with a feed of 0.25 mm/rev, depth of cut of 4 mm and cutting velocity of 90m/min. it is observed that the main (tangential) cutting force is perpendicular to the friction force acting at the chip-tool interface. The main(tangential) cutting force is 1500 N.

  1. The normal force acting the chip-tool interface in N is








  1. View Hint View Answer Discuss in Forum

    N = Fc .cosα – FT .sinα
    ∴ α = 0
    N = Fc = 1500 N

    Correct Option: B

    N = Fc .cosα – FT .sinα
    ∴ α = 0
    N = Fc = 1500 N

  1. The orthogonal rake angle of the cutting tool in degree is








  1. View Hint View Answer Discuss in Forum

    D = 100 mm feed, f = 0.25 mm/rev d = 4 mm, V = 90m/min, Fc = 1500 N
    α = 0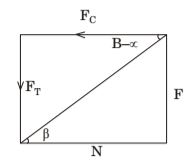

    Correct Option: A

    D = 100 mm feed, f = 0.25 mm/rev d = 4 mm, V = 90m/min, Fc = 1500 N
    α = 0

  1. Minimum shear-strain in orthogonal turning with a cutting tool of zero rake angle is








  1. View Hint View Answer Discuss in Forum

    Shear strain , τ =
    cosα
    sinφ.cos( φ - α )

    where, α = 0 = rake angle , φ = shear angle
    ∴ τ =
    1
    sinθcosθ

    ∴ T = sinφcosφ
    dt
    		 = cos ²φ - sin ²φ
    dφ

    or φ = 45°
    ∴ τmin =
    1
    { sin (π /4).cos(π /4) }

    ∴ τmin =
    1
    		 = 2
    { sin (1 /√2) × (1 /√2) }

    Correct Option: D

    Shear strain , τ =
    cosα
    sinφ.cos( φ - α )

    where, α = 0 = rake angle , φ = shear angle
    ∴ τ =
    1
    sinθcosθ

    ∴ T = sinφcosφ
    dt
    		 = cos ²φ - sin ²φ
    dφ

    or φ = 45°
    ∴ τmin =
    1
    { sin (π /4).cos(π /4) }

    ∴ τmin =
    1
    		 = 2
    { sin (1 /√2) × (1 /√2) }