Industrial Engineering Miscellaneous Easy Questions and Answers | Page - 7

Industrial Engineering Miscellaneous

The sale of cycles in a shop in four consecutive months are given as 70, 68, 82, 95. Exponentially smoothing average method with a smoothing factor of 0.4 is used in forecasting. The expected number of sales in the next month is

1. 59
1. 72
1. 86
1. 136

View Hint View Answer Discuss in Forum

F_t+1 = D_t + α(1 – α) D_t–1 + α(1 – α) ² D_t–2
F_t+1 = 0.4 (95) + 0.4 (1 – 0.4)² + α(1 – α)³ D_t–3 + (0.4) (1 – 0.4)² × 68 + (0.4) (1 – 0.4)³ × 70
F_{t–1_{= 73.52 units}}

Correct Option: C

F_t+1 = D_t + α(1 – α) D_t–1 + α(1 – α) ² D_t–2
F_t+1 = 0.4 (95) + 0.4 (1 – 0.4)² + α(1 – α)³ D_t–3 + (0.4) (1 – 0.4)² × 68 + (0.4) (1 – 0.4)³ × 70
F_{t–1_{= 73.52 units}}

A regression model is used to express a variable V as a function of another variable X, this implies that

1. There is a causal relationship between Y and X
1. A value of X may be used to estimate a value of Y
1. Values of X exactly determine values of Y
1. There is no causal relationship between Y and X

View Hint View Answer Discuss in Forum

NA

Correct Option: A

NA

In an assembly line for assembling toys, five workers are assigned tasks which take times of 10, 8, 6, 9 and 10 minutes respectively. The balance delay for line is

1. 43.3%
1. 14.8%
1. 14.0%
1. 16.3%

View Hint View Answer Discuss in Forum

Assuming cycle time = 10 + 8 + 6 + 9 + 10 = 43
Balance delay = 1 - ∑ t_i = 1- 43 = 0.14
n × t_e 5 × 10

= 14%

Correct Option: C

Assuming cycle time = 10 + 8 + 6 + 9 + 10 = 43
Balance delay = 1 - ∑ t_i = 1- 43 = 0.14
n × t_e 5 × 10

= 14%

If at the optimum in a linear programming problem, a dual variable corresponding to a particular primal constraint is zero, then it means that

1. Right hand side of the primal constraint can altered without affecting the optimum solution
1. Changing the right hand side of the primal constraint will disturb the optimum solution
1. The objectives function is unbounded
1. The problem is degenerate

View Hint View Answer Discuss in Forum

NA

Correct Option: C

NA

A manufacturer produces two types of products, 1 and 2, at production levels of x₁ and x₂ respectively. The profit is given is 2x₁ + 5x₂. The production constraints are :
x₁ + 3x₂ < 40
3x₁ + x₂ < 24
x₁ + x₂ < 10
x₁ > 0 , x₂ > 0
The maximum profit which can meet the constraints is

1. 29
1. 38
1. 44
1. 75

View Hint View Answer Discuss in Forum

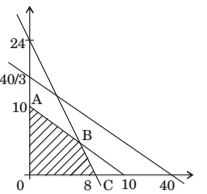
Feasible Region (0– A – B – C– 0)
At point (A) 0, 10)
Z = 2 (0) + 5 (10) = 50
At point B (7,3)
Z = 2(7) + 5(3) = 2y
At point C (8, 0)
Z = 2(16) + 5(0) = (16) 2
⇒ 32
Hence maximum profit is Z_max = 50
No correct option is given.

Correct Option: C

Feasible Region (0– A – B – C– 0)
At point (A) 0, 10)
Z = 2 (0) + 5 (10) = 50
At point B (7,3)
Z = 2(7) + 5(3) = 2y
At point C (8, 0)
Z = 2(16) + 5(0) = (16) 2
⇒ 32
Hence maximum profit is Z_max = 50
No correct option is given.