Industrial Engineering Miscellaneous

Industrial Engineering Miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Industrial Engineering

Industrial Engineering Miscellaneous
  1. In PERT analysis a critical activity has








  1. View Hint View Answer Discuss in Forum

    Earliest Start =
    Least Start
    		 = 0
    Float

    Correct Option: B

    Earliest Start =
    Least Start
    		 = 0
    Float

  1. A dummy activity is used in PERT network to describe








  1. View Hint View Answer Discuss in Forum

    Dummy activities often have a zero completion time & are used to represents precendence relationship.

    Correct Option: A

    Dummy activities often have a zero completion time & are used to represents precendence relationship.

  1. In PERT, the distribution of activity times is assumed to be








  1. View Hint View Answer Discuss in Forum

    NA

    Correct Option: C

    NA

  1. A company produces two types of toys: P and Q. Production time of Q is twice that of P and the company has a maximum of 2000 time units per day. The supply of raw material is just sufficient to produce 1500 toys (of any type) per day. Toy type Q requires an electric switch which is available @ 600 pieces per day only. The company makes a profit of Rs. 3 and Rs. 5 on type P and Q respectively. For maximization of profits, the daily production quantities of P and Q toys should respectively be








  1. View Hint View Answer Discuss in Forum

    Zmax = 3P + 5Q
    subject to P + 2Q ≤ 2000
    P + Q ≤ 1500
    Q ≤ 600
    P, Q ≥ 0

    Feasible solution (O A B C D)
    Since At point A (1500,0)
    Z = 3 × 1500 + 5 × 0 = 4500
    At Point B (1000, 500)
    Z = 3 × 1000 + 5 × 500 = 5500
    At point C (800, 600)
    Z = 3 × 800 + 5 × 600 = 5400
    At Point O (0, 600)
    Z = 3 × 0 + 5 × 600 = 3000
    Hence Z in maximum at B (1000,500)
    P = 1000 units and Q = 500 units

    Correct Option: A

    Zmax = 3P + 5Q
    subject to P + 2Q ≤ 2000
    P + Q ≤ 1500
    Q ≤ 600
    P, Q ≥ 0

    Feasible solution (O A B C D)
    Since At point A (1500,0)
    Z = 3 × 1500 + 5 × 0 = 4500
    At Point B (1000, 500)
    Z = 3 × 1000 + 5 × 500 = 5500
    At point C (800, 600)
    Z = 3 × 800 + 5 × 600 = 5400
    At Point O (0, 600)
    Z = 3 × 0 + 5 × 600 = 3000
    Hence Z in maximum at B (1000,500)
    P = 1000 units and Q = 500 units

  1. A manufacturer produces two types of products, 1 and 2, at production levels of x1 and x2 respectively. The profit is given is 2x1 + 5x2. The production constraints are :
    x1 + 3x2 < 40
    3x1 + x2 < 24
    x1 + x2 < 10
    x1 > 0 , x2 > 0
    The maximum profit which can meet the constraints is








  1. View Hint View Answer Discuss in Forum


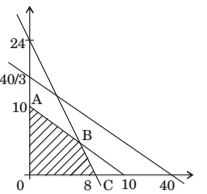
    Feasible Region (0– A – B – C– 0)
    At point (A) 0, 10)
    Z = 2 (0) + 5 (10) = 50
    At point B (7,3)
    Z = 2(7) + 5(3) = 2y
    At point C (8, 0)
    Z = 2(16) + 5(0) = (16) 2
    ⇒ 32
    Hence maximum profit is Zmax = 50
    No correct option is given.

    Correct Option: C


    Feasible Region (0– A – B – C– 0)
    At point (A) 0, 10)
    Z = 2 (0) + 5 (10) = 50
    At point B (7,3)
    Z = 2(7) + 5(3) = 2y
    At point C (8, 0)
    Z = 2(16) + 5(0) = (16) 2
    ⇒ 32
    Hence maximum profit is Zmax = 50
    No correct option is given.