-
The length of each side of a rhombus is equal to the length of the side of a square whose diagonal is 40√2 cm. If the length of the diagonals of the rhombus are in the ratio 3 : 4, then its area (in cm²) is
-
- 1550
- 1600
- 1535
- 1536
- 1550
Correct Option: D
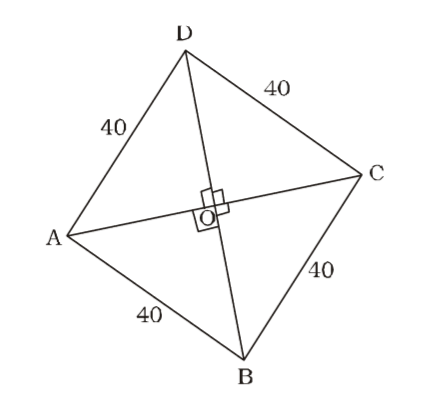
Using Rule 12,
Side of rhombus = side of square.
= √2a = 40√2a ⇒ a = 40
⇒ AC ⊥ BD; ∠AOD = 90°
Let AC = 3x and BD = 4x cm
| ∴ AO = | ; OD = 2x cm | |
| 2 |
From ∆ AOD,
OA² + OD² = AD²
 |  | ² | + 4x² = 40² | |
| 2 |
⇒ 9x² + 16x² = 1600 × 4
⇒ 25x² = 6400
⇒ x² = 6400 ÷ 25 = 256
⇒ x = √256 = 16
∴ AC = 3 × 16 = 48 cm
and BD = 4 × 16 = 64 cm
| ∴ Area of rhombus = | × AC × BD | |
| 2 |
| = | × 48 × 64 = 1536 sq.cm. | |
| 2 |

