One of the angles of a right-angled triangle is 15°, and

Home » Aptitude » Mensuration » Question

One of the angles of a right-angled triangle is 15°, and the hypotenuse is 1 metre. The area of the triangle (in square cm.) is

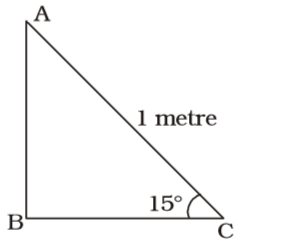
sin 15° = sin (45° – 30°)
= sin 45° × cos 30° – cos 45° × sin 30°

=	1	×	√3	-	1	×	1
	√2		2		√2		2

=	√3	-	1	=	√3 - 1
	2√2		2√2		2√2

and cos 15° = cos (45°– 30°)
= cos 45°. cos 30° + sin 45°. sin 30°

=	1	×	√3	+	1	×	1
	√2		2		√2		2

=	√3	+	1	=	√3 + 1
	2√2		2√2		2√2

∴ AB = AC sin 15°

=	√3 - 1	metre
	2√2

BC = AC cos 15° =	√3 + 1	metre
	2√2

∴ Area of ∆ABC =	1	× AB × BC
	2

=		1	×	√3 - 1	×	√3 + 1		square metre
		2		2√2		2√2

=		3 - 1		square metre
		16

=	1	square metre
	8

=	10000	= 1250 square metre
	8