-
ABCD is a parallelogram in which diagonals AC and BD intersect at O. If E, F, G and H are the mid points of AO, DO, CO and BO respectively, then the ratio of the perimeter of the quadrilateral EFGH to the perimeter of parallelogram ABCD is
-
- 1 : 4
- 2 : 3
- 1 : 2
- 1 : 3
- 1 : 4
Correct Option: C
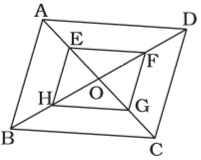In ∆OAB,
Mid-point of OA = E
Mid-point of OB = H
∴ EH || AB and HE = 1/2 AB
Similarly, HG = 1/2 BC,
FG = 1/2 CD and EF = 1/2 AD
∴ EH + HG + FG + EF = 1/2 (AB + BC + CD + AD)
⇒ Perimeter of EFGH = 1/2 × Perimeter of ABCD
∴ Required ratio = 1: 2
