A circle is inscribed in a square whose length of the diagonal

Home » Aptitude » Mensuration » Question

A circle is inscribed in a square whose length of the diagonal is 12√2 cm. An equilateral triangle is inscribed in that circle. The length of the side of the triangle is

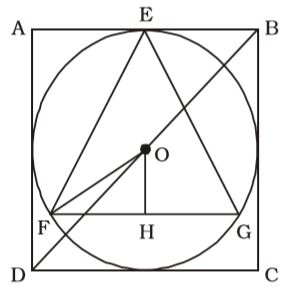
Side of square =	1	× 12√2 cm = 12 cm
	√2

∴ Radius of circle =	12	= 6 cm
	2

AB = 2x cm
∴ FH = x cm
∴ From ∆OFH,

cos 30° =	FH
	OF

⇒	√3	=	x
	2		6

⇒ x =	6 × √3	= 3√3
	2

∴ Length of side = 6√3 cm