-
The base of a right prism is a quadrilateral ABCD. Given that AB = 9 cm, BC = 14 cm, CD = 13 cm, DA = 12 cm and ∠DAB = 90°. If the volume of the prism be 2070 cm³, then the area of the lateral surface is
-
- 720 cm²
- 810 cm²
- 1260 cm²
- 2070 cm²
- 720 cm²
Correct Option: A
Area of base = Area of ∆ABD + Area of ∆BCD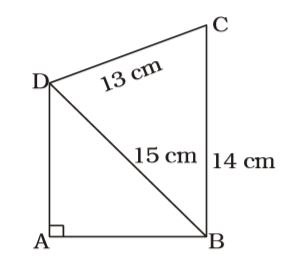
In, ∆ABD
BD = √AB² + AD² = √9² + 12²
= √81 + 144 = √225 = 15 cm
Area of ∆ABD
| Semi-perimeter (s) = | = | = 21 | ||
| 2 | 2 |
∴ Area of ∆BCD
= √s(s - a)(s - b)(s - c)
= √21(21 - 13)(21 - 14)(21 - 15)
= √21 × 8 × 7 × 6
= 21 × 4 = 84 sq. cm
Area of quadrilateral ABCD = 54 + 84 = 138 sq, cm
| ∴ Height of prism = | = | = 15 cm. | ||
| Area of base | 138 |
Perimeter of base = (9 + 14 + 13 +12) cm = 48 cm
∴ Area of lateral surfaces = perimeter × height
= 48 × 15 = 720 sq. cm.

