171. An open loop control system results in a response of e^{– 2t} (sin5t + cos5t) for a unit impulse input. The DC gain of the control system is ______.

1. 1. 241

   
   
   

   2. 0.241

   
   
   

   3. 41

   
   
   

   4. 0.21

   
   
   

---

1. View Hint View Answer Discuss in Forum

   g(t) = e ^{– 2} [sin5t + cos5t]
   Taking lapcase transform of g(t),
   

   ∴ G(s) =	5	+	s + 2
   	(s + 2)2 + 52		(s + 2)2 + 52

   
   For DC gain, |G(s)| _{s = 0}
   

   G(0) =	5	+	2	=	7
   	22 + 52		22 + 52		29

   
   

   Correct Option: B

   g(t) = e ^{– 2} [sin5t + cos5t]
   Taking lapcase transform of g(t),
   

   ∴ G(s) =	5	+	s + 2
   	(s + 2)2 + 52		(s + 2)2 + 52

   
   For DC gain, |G(s)| _{s = 0}
   

   G(0) =	5	+	2	=	7
   	22 + 52		22 + 52		29

   
   

---

172. For the given system, it is desired that the system be stable. The minimum value of α for this condition is _________.
     
     

1. 1. 320.67

   
   
   

   2. 618

   
   
   

   3. 61.018

   
   
   

   4. 0.618

   
   
   

---

1. View Hint View Answer Discuss in Forum

   From the characteristic equation
   1 + G(s) H(s) = 0
   

   1 +	(s + α)	= 0
   	s3 + (1 + α)s2 + (α - 1)s + (1 - α)

   
   ∴ s³ + (1 + α)s² + αs +1 = 0
   By Routh Hurwitz criteria
   (1 + α) α >1
   (α² + α – 1) > 0
   ∴ α = 0.618 & – 0.618
   But for system to be stable
   α = 0.618
   

   Correct Option: D

   From the characteristic equation
   1 + G(s) H(s) = 0
   

   1 +	(s + α)	= 0
   	s3 + (1 + α)s2 + (α - 1)s + (1 - α)

   
   ∴ s³ + (1 + α)s² + αs +1 = 0
   By Routh Hurwitz criteria
   (1 + α) α >1
   (α² + α – 1) > 0
   ∴ α = 0.618 & – 0.618
   But for system to be stable
   α = 0.618
   

---

---

173. The Bode magnitude plot of the transfer function
     

     G(s) =

     K(1 + 0.5s)(1 + as)

     I shown below :

     s

     1 +

     s

     (1 + bs)

     1 +

     s

     8

     36

     
     

     Note that – 6 dB/octave = – 20dB/decade. The value of	a	is ______________.
     	bK

     
     
     

1. 1. 0.75

   
   
   

   2. 25

   
   
   

   3. 7.5

   
   
   

   4. None of the above

   
   
   

---

1. View Hint View Answer Discuss in Forum

   From the magnitude plot,
   

   G(s) =

   K

   1 +

   S

   1 +

   S

   2

   4

   S

   1 +

   S

   1 +

   S

   1 +

   S

   8

   24

   36

   
   Now comparing with given transfer function
   

   a =	1	; b =	1
   	4		24

   
   For finding K:
   
   K = (ω)n : where n is no. of poles from the given plot
   ∴ K = (8)¹
   

   Now ,	a	=	1	× 8 = 0.75
   	bk		24

   
   

   Correct Option: A

   From the magnitude plot,
   

   G(s) =

   K

   1 +

   S

   1 +

   S

   2

   4

   S

   1 +

   S

   1 +

   S

   1 +

   S

   8

   24

   36

   
   Now comparing with given transfer function
   

   a =	1	; b =	1
   	4		24

   
   For finding K:
   
   K = (ω)n : where n is no. of poles from the given plot
   ∴ K = (8)¹
   

   Now ,	a	=	1	× 8 = 0.75
   	bk		24

   
   

---

174. The closed-loop transfer function of a system is T(s) =	4
     	(s2 + 0.4s + 4)

     
     The steady state error due to unit step input is ____.

1. 1. 0 to 0

   
   
   

   2. 4 to 3

   
   
   

   3. 1 to 5

   
   
   

   4. None of the above

   
   
   

---

1. View Hint View Answer Discuss in Forum

   T(s) =	C(s)	=	4
   	R(s)		s2 + 0.4s + 4

   
   

   ⇒	R(s) - C(s)	=	E(s)	=	s2 + 0.4s
   	R(s)		R(s)		s2 + 0.4s + 4

   
   Steady- state error
   
   

   Here , R(s) =	1
   	s

   
   
   

   Correct Option: A

   T(s) =	C(s)	=	4
   	R(s)		s2 + 0.4s + 4

   
   

   ⇒	R(s) - C(s)	=	E(s)	=	s2 + 0.4s
   	R(s)		R(s)		s2 + 0.4s + 4

   
   Steady- state error
   
   

   Here , R(s) =	1
   	s

   
   
   

---

---

175. The frequency response of G(s) =	1	plotted in the complex G(jω)
     	[s(s + 1)(s + 2)]

     
     plane (for 0 < ω < ∞) is

1. 1. 
      

   
   
   

   2. 
      

   
   
   

   3. 
      

   
   
   

   4. 

   
   
   

---

1. View Hint View Answer Discuss in Forum

   G(s) =	1
   	s(s + 1)(s + 2)

   
   

   G(jω) =	1
   	jω(jω + 1)(jω + 2)

   
   

   M =	1
   	ω√ω² + 1 √ω² + 4

   
   

   ∠ φ = -90 - tan-1ω - tan-1	ω
   	2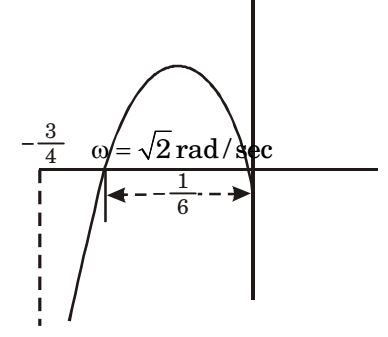

   
   
   For ω = 0, M = ∞ ; ∠ φ = – 90
   For ω = ∞, M = 0; ∠ φ = – 90 – 90 – 90 = – 270
   So Cutting Real Axis
   Imaginary part of G(jω) = 0
   i.e. Img {G(jω)} = 0
   

   ⇒ Im		1		= 0
   		jω(-ω2 + 3)ω + 2

   
   

   ⇒ Im		1		= 0
   		-jω3 - 3ω2 + 2jω

   
   

   ⇒ Im		1		= 0
   		- 3ω2 + j(2ω - ω3)

   
   

   ⇒ Im		-3ω2 - j(2ω - ω3)		= 0
   		(3ω2)2 + (2ω - ω3)2

   
   ∴ 2ω – ω³ = 0
   ⇒ ω² = 2 . ω = 0
   Neglecting ω = 0, we have
   ω = √2
   

   ∴ M |at ω = √2 =	1	=	1	⇒	1	<		3
   	√2 √3 √2 + 4		√36		6			4

   
   

   Correct Option: A

   G(s) =	1
   	s(s + 1)(s + 2)

   
   

   G(jω) =	1
   	jω(jω + 1)(jω + 2)

   
   

   M =	1
   	ω√ω² + 1 √ω² + 4

   
   

   ∠ φ = -90 - tan-1ω - tan-1	ω
   	2

   
   
   For ω = 0, M = ∞ ; ∠ φ = – 90
   For ω = ∞, M = 0; ∠ φ = – 90 – 90 – 90 = – 270
   So Cutting Real Axis
   Imaginary part of G(jω) = 0
   i.e. Img {G(jω)} = 0
   

   ⇒ Im		1		= 0
   		jω(-ω2 + 3)ω + 2

   
   

   ⇒ Im		1		= 0
   		-jω3 - 3ω2 + 2jω

   
   

   ⇒ Im		1		= 0
   		- 3ω2 + j(2ω - ω3)

   
   

   ⇒ Im		-3ω2 - j(2ω - ω3)		= 0
   		(3ω2)2 + (2ω - ω3)2

   
   ∴ 2ω – ω³ = 0
   ⇒ ω² = 2 . ω = 0
   Neglecting ω = 0, we have
   ω = √2
   

   ∴ M |at ω = √2 =	1	=	1	⇒	1	<		3
   	√2 √3 √2 + 4		√36		6			4

   
   

---