106. The transfer function C/R of the system shown in the figure is
     

1. 1. 	G1 G2 H2
      	H1 (1 + G1 G2 H2)

   
   
   

   2. 	G1 H2
      	H1 (1 + G1 G2 H2)

   
   
   

   3. 	G2 H2
      	H1 (1 + G1 G2 H1)

   
   
   

   4. 	G2 H1
      	H2 (1 + G1 G2 H2)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   It is a very simple block diagram and simply by inspection we see that
   

   	C(s)	=	1		H2G1
   	R(s)		H1		(1 + H2G1G2)

   Correct Option: B

   It is a very simple block diagram and simply by inspection we see that
   

   	C(s)	=	1		H2G1
   	R(s)		H1		(1 + H2G1G2)

---

107. A system is represented by the block diagram given in the figure :
     
     Which of the following represents the input output relationship of the above diagram?
     

1. 1. 
      

   
   
   

   2. 
      

   
   
   

   3. 
      

   
   
   

   4. 

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: D

   NA

---

---

108. In the given figure, spring constant is K, viscous friction coefficient is B, mass is M and the system output motions is x(t) corresponding to input force F (t).
     
     Which of the following parameters related to the above system?
     

     1. Time constant =	1
     	M

     
     

     2. Damping coefficient =	B
     	2 √KM

     
     

     3. Natural frequency of oscillation = √	K
     	M

     
     Select the correct answer using the codes given below :
     

1. 1. 1, 2 and 3

   
   
   

   2. 1 and 2

   
   
   

   3. 2 and 3

   
   
   

   4. 1 and 3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   F(t) = M	d2x(t)	+ B	dx(t)	+ Kx(t)
   	dt2		dt

   
   The characteristic equation is,
   Ms² + Bs + K = 0
   or s ² + 2 ω_n s + ω_n ² = 0
   
   Thus statements 2 and 3 are correct.

   Correct Option: C

   F(t) = M	d2x(t)	+ B	dx(t)	+ Kx(t)
   	dt2		dt

   
   The characteristic equation is,
   Ms² + Bs + K = 0
   or s ² + 2 ω_n s + ω_n ² = 0
   
   Thus statements 2 and 3 are correct.

---

109. The magnitude Bode plot of a network is shown in the figure
     
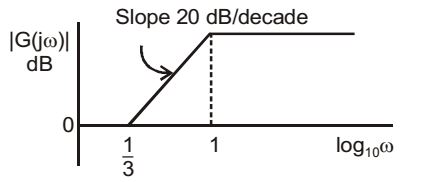
     The maxi mum phase angle φ_m and t he corresponding gain G_m respectively, are
     

1. 1. – 30° and 1.73dB

   
   
   

   2. – 30° and 4.77dB

   
   
   

   3. +30° and 4.77dB

   
   
   

   4. +30° and 1.73dB

   
   
   

---

1. View Hint View Answer Discuss in Forum

   G(s) = k.	(1 + 3s)
   	(1 + s)

   
   

   G(s) =		3k.		s +	1
   					3
   			(s + 1)

   
   Here k = 1
   

   	1	=	1	⇒	1	= 1
   	T		3		αT

   
   

   ωm =	1	; α =	1
   	√3		3

   
   
   G _m | _{in dB} = 20 log √3 = 4.77 dB
   

   φm = sin-1			1 - α
   			1 + α

   
   

   α = 1 / 3 = sin-1		1 - 1 / 3		= sin-1		1
   		1 + 1 / 3				2

   
   φ_m = 30°
   

   Correct Option: C

   G(s) = k.	(1 + 3s)
   	(1 + s)

   
   

   G(s) =		3k.		s +	1
   					3
   			(s + 1)

   
   Here k = 1
   

   	1	=	1	⇒	1	= 1
   	T		3		αT

   
   

   ωm =	1	; α =	1
   	√3		3

   
   
   G _m | _{in dB} = 20 log √3 = 4.77 dB
   

   φm = sin-1			1 - α
   			1 + α

   
   

   α = 1 / 3 = sin-1		1 - 1 / 3		= sin-1		1
   		1 + 1 / 3				2

   
   φ_m = 30°
   

---

---

110. The open loop poles of a third order unity feedback system are at 0, – 1, – 2. Let the frequency corresponding to the point where the root locus of the system transits to unstable region be K. Now suppose we introduce a zero in the open loop transfer function at – 3, while keeping all the earlier open loop poles intact. Which one of the following is TRUE about the point where the root locus of the modified system transits to unstable region?
     

1. 1. It corresponds to a frequency greater than K
      

   
   
   

   2. It corresponds to a frequency less than K

   
   
   

   3. It corresponds to a frequency K

   
   
   

   4. Root locus of modified system never transits

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Open loop transfer function of a third order unity feedback system
   

   G(s) =	K
   	s (s + 1)(s + 2)

   
   Now zero is introduce at – 3.
   Modified transfer function,
   

   G(s) =	K(s + 3)
   	s (s + 1)(s + 2)

   
   Closed loop characteristic equation,
   1 + G(s) = 0
   

   1 +	K(s + 3)	= 0
   	s (s + 1)(s + 2)

   
   s(s + 1)(s + 2) + K(s + 3) = 0
   s³ + 3s ² + 2s + Ks + 3K = 0
   s³ + 3s² + (K + 2)s + 3K = 0
   Routh array corresponding to characteristic equation,
   
   For every value of K > 0 I st column of the array are positive.
   Therefore, Root locus of modified system never transits to unstable region.

   Correct Option: D

   Open loop transfer function of a third order unity feedback system
   

   G(s) =	K
   	s (s + 1)(s + 2)

   
   Now zero is introduce at – 3.
   Modified transfer function,
   

   G(s) =	K(s + 3)
   	s (s + 1)(s + 2)

   
   Closed loop characteristic equation,
   1 + G(s) = 0
   

   1 +	K(s + 3)	= 0
   	s (s + 1)(s + 2)

   
   s(s + 1)(s + 2) + K(s + 3) = 0
   s³ + 3s ² + 2s + Ks + 3K = 0
   s³ + 3s² + (K + 2)s + 3K = 0
   Routh array corresponding to characteristic equation,
   
   For every value of K > 0 I st column of the array are positive.
   Therefore, Root locus of modified system never transits to unstable region.

---