116. The second order dynamic system
     

     	dX	= PX + Qu y = RX
     	dt

     
     has the matrices P, Q and R as follows :
     

     P =		-1			1		, Q =		0		, R = [0   1]
     		0			-3				1

     
     The system has the following controllability and observability properties :
     

1. 1. Controllable and observable

   
   
   

   2. Not controllable but observable

   
   
   

   3. Controllable but not observable

   
   
   

   4. Not controllable and not observable

   
   
   

---

1. View Hint View Answer Discuss in Forum

   For controllability,
   M_C = [Q PQ]
   

   MC =		0			1
   		1			- 3

   
   
   Therefore, the system is Controllable.
   Now, for observability.
   

   M0 = [RT RT pT ] =		0			0
   		1			- 3

   
   
   Therefore, the system is not observable.

   Correct Option: C

   For controllability,
   M_C = [Q PQ]
   

   MC =		0			1
   		1			- 3

   
   
   Therefore, the system is Controllable.
   Now, for observability.
   

   M0 = [RT RT pT ] =		0			0
   		1			- 3

   
   
   Therefore, the system is not observable.

---

117. The signal flow graph of a system is shown below. U(s) is the input and C(s) is the output
     
     Assuming, h₁ = b₁ and h₀ = b₀ – b₁ a₁, then input-output

     transfer function, G(s) =	C(s)	of the system is given by
     	U(s)

1. 1. G(s) =	b0s + b1
      	s2 + a0s + a1

   
   
   

   2. G(s) =	a1s + a0
      	s2 + b1s + b0

   
   
   

   3. G(s) =	b1s + b0
      	s2 + a1s + a0

   
   
   

   4. G(s) =	a0s + a1
      	s2 + b0s + b1

   
   
   

---

1. View Hint View Answer Discuss in Forum

   From the signal flow graph, G(s) =	C(s)
   	U(s)

   
   By mason’s gain relation,
   

   Transfer function =	P1 ∆1 + P2 ∆2 + .......
   	∆

   
   

   P1 =	h1	; P2 =	h0
   	S		s2

   
   

   ∆1 =		1 +	a1		; ∆2 = 1 ;
   			s

   
   

   ∆ = 1 +	a1	+	a0
   	s		s2

   
   

   Transfer function =	h1		1 +	a1		+	b0
   	s			s			s2	=	b1s + b0
   	1 +	a1	+	a0					s2 + a1s + a0
   		s		s2

   
   

   Correct Option: C

   From the signal flow graph, G(s) =	C(s)
   	U(s)

   
   By mason’s gain relation,
   

   Transfer function =	P1 ∆1 + P2 ∆2 + .......
   	∆

   
   

   P1 =	h1	; P2 =	h0
   	S		s2

   
   

   ∆1 =		1 +	a1		; ∆2 = 1 ;
   			s

   
   

   ∆ = 1 +	a1	+	a0
   	s		s2

   
   

   Transfer function =	h1		1 +	a1		+	b0
   	s			s			s2	=	b1s + b0
   	1 +	a1	+	a0					s2 + a1s + a0
   		s		s2

   
   

---

---

118. A single-input single-output feedback system has forward transfer function G(s) and feedback transfer funct i on H (s). It is given that |G(s).H(s)|< 1. Which of the following is true about the stability of the system?
     

1. 1. The system is always stable

   
   
   

   2. The system is stable if all zeros of G(s).H(s) are in left half of the s-plane

   
   
   

   3. The system is stable if all poles of G(s).H(s) are in left half of the s-plane

   
   
   

   4. It is not possible to say whether or not the system is stable from the information given

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: A

   NA

---

119. The block diagram of a system is shown in the figure
     
     If the desired transfer function of the system is
     

     	C(s)	=	s
     	R(s)		s2 + s + 1

     
     Then G(s) is
     

1. 1. 1

   
   
   

   2. s

   
   
   

   3. 1 / s
      

   
   
   

   4. 	-s
      	s3 + s2 - s - 2

      
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   If G(s) = S
   

   	C(s)	=	S
   	R(s)		s2 + s + 2

   Correct Option: B

   
   If G(s) = S
   

   	C(s)	=	S
   	R(s)		s2 + s + 2

---

---

120. The transfer function of a second order real system with a perfectly flat magnitude response of unity has a pole at (2 – j3). List all the poles and zeroes.

1. 1. Poles at (2 ± j3), no zeroes
      

   
   
   

   2. Poles at (±2 – j3), one zero at origin

   
   
   

   3. Poles at (2 – j3), (– 2 + j3), zeroes at (– 2 – j3), (2 + j3)

   
   
   

   4. Poles at (2 ± j3), zeroes at (– 2 ± j3)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   System is second order
   It means, number of poles = 2
   System has perfectly flat magnitude response.
   It means, It is all pass system
   In all pass system,
   Poles and zeros are mirror image about Imaginary axis,
   One pole = (2 – j3)
   Other pole = (2 + j3)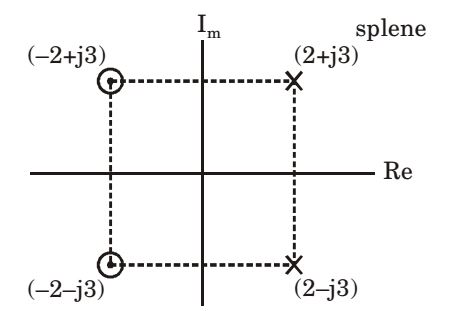
   
   Therefore
   poles at (2 ± j3)
   zeros at (– 2 ± j3)

   Correct Option: D

   System is second order
   It means, number of poles = 2
   System has perfectly flat magnitude response.
   It means, It is all pass system
   In all pass system,
   Poles and zeros are mirror image about Imaginary axis,
   One pole = (2 – j3)
   Other pole = (2 + j3)
   
   Therefore
   poles at (2 ± j3)
   zeros at (– 2 ± j3)

---