Correct Option: A

G(s) =	1
	s(s + 1)(s + 2)

G(jω) =	1
	jω(jω + 1)(jω + 2)

M =	1
	ω√ω² + 1 √ω² + 4

∠ φ = -90 - tan-1ω - tan-1	ω
	2

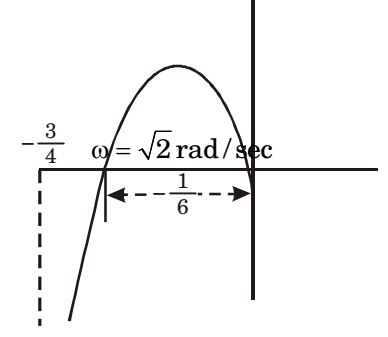
For ω = 0, M = ∞ ; ∠ φ = – 90
For ω = ∞, M = 0; ∠ φ = – 90 – 90 – 90 = – 270
So Cutting Real Axis
Imaginary part of G(jω) = 0
i.e. Img {G(jω)} = 0

⇒ Im		1		= 0
		jω(-ω2 + 3)ω + 2

⇒ Im		1		= 0
		-jω3 - 3ω2 + 2jω

⇒ Im		1		= 0
		- 3ω2 + j(2ω - ω3)

⇒ Im		-3ω2 - j(2ω - ω3)		= 0
		(3ω2)2 + (2ω - ω3)2

∴ 2ω – ω³ = 0
⇒ ω² = 2 . ω = 0
Neglecting ω = 0, we have
ω = √2

∴ M |at ω = √2 =	1	=	1	⇒	1	<		3
	√2 √3 √2 + 4		√36		6			4