Control system miscellaneous
- The Nyquist plot of a loop transfer funct ion G(jω) H(jω) of a system encloses the (– 1, j0) point. The gain margin of the system is
-
View Hint View Answer Discuss in Forum
Gain margin of the system for which Nyquist plot of a loop tr ansfer function G(jω) H(jω) encloses (– 1, + j0) point is less than zero.
Correct Option: A
Gain margin of the system for which Nyquist plot of a loop tr ansfer function G(jω) H(jω) encloses (– 1, + j0) point is less than zero.
- The position and velocity error coefficients for the system of transfer function
G(s) = 50 (1 + 0.1s)(1 + 2s)
respectively are
-
View Hint View Answer Discuss in Forum
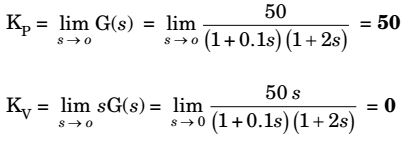
Correct Option: C
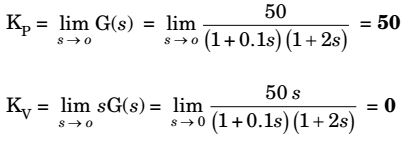
- Consider the following statements regarding timedomain analysis of a control system :
1. Derivative control improves system’s transient performance
2. I ntegral control does not improve system’s steady state performance
3. I ntegral control can convert a second order system into a third order system
Of these statements
-
View Hint View Answer Discuss in Forum
For same KV, the natural frequency ωn remains unchanged in derivative control while damping is increased.
Thus it improves the transient response.
Integral compensator introduces a term 1/s, thus changes second order to third order.Correct Option: B
For same KV, the natural frequency ωn remains unchanged in derivative control while damping is increased.
Thus it improves the transient response.
Integral compensator introduces a term 1/s, thus changes second order to third order.
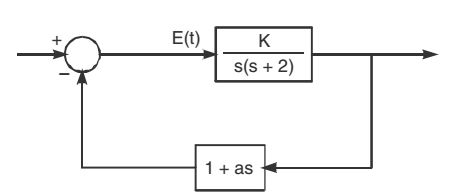
- For the system shown in the figure, with a damping ratio ξ of 0.7. and undamped natural frequency ωn of 4 rad / sec, the values of K and a are
-
View Hint View Answer Discuss in Forum
M(s) = G(s) = K / s ( + 2) 1 + G(s) H(s) 1 + (1 + as) K / s (s + 2)
The characteristic equation is
s (s + 2) + K (1 + as) = 0
⇒ s2 + s (2 + aK) + K = 0
Compare with equation s 2 + 2 ξ ωn s + ωn2 = 0, we get
K = ωn 2 = 42 = 16
∴ 2 ξ ωn = (2 + aK)⇒ a = 2 × 0.7 × 4 - 2 = 3.6 = 0.225 16 16
Correct Option: C
M(s) = G(s) = K / s ( + 2) 1 + G(s) H(s) 1 + (1 + as) K / s (s + 2)
The characteristic equation is
s (s + 2) + K (1 + as) = 0
⇒ s2 + s (2 + aK) + K = 0
Compare with equation s 2 + 2 ξ ωn s + ωn2 = 0, we get
K = ωn 2 = 42 = 16
∴ 2 ξ ωn = (2 + aK)⇒ a = 2 × 0.7 × 4 - 2 = 3.6 = 0.225 16 16
- The closed-loop transfer function of a control system is given by
C(s) = 2(s - 1) R(s) (s + 2)(s + 1)
For a unit step input the output is
-
View Hint View Answer Discuss in Forum
C(s) = 2(s - 1) , R(s) = 1 R(s) (s + 2)(s + 1) s Hence , C(s) = 2(s - 1) s(s + 1)(s + 2) = K1 + K2 + K3 s s + 1 s + 2 
Hence , C(s) = -1 + 4 - 3 s s + 1 s + 2
⇒ c(t) = [– 1 + 4e– t – 3e– 2t]Correct Option: A
C(s) = 2(s - 1) , R(s) = 1 R(s) (s + 2)(s + 1) s Hence , C(s) = 2(s - 1) s(s + 1)(s + 2) = K1 + K2 + K3 s s + 1 s + 2 
Hence , C(s) = -1 + 4 - 3 s s + 1 s + 2
⇒ c(t) = [– 1 + 4e– t – 3e– 2t]

