Computer networks miscellaneous

Computer networks miscellaneous

Easy Questions

Computer Networks

Computer networks miscellaneous
  1. Consider a token ring network with a length of 2 km having 10 stations including a monitoring station. The propagation speed of the signal is 2 × 108 m/s and the token transmission time is ignored. If each station is allowed to hold the token for 2 msec, the minimum time for which the monitoring station should wait (in m sec)before assuming that the token is lost is _______.








  1. View Hint View Answer Discuss in Forum

    28 to 30 sec.

    Correct Option: A

    28 to 30 sec.

  1. A bit-stuffing based framing protocol uses an 8-bit delimiter pattern of 01111110. If the output bit-string after stuffing is 01111100101, then the input bit-string is








  1. View Hint View Answer Discuss in Forum

    Output bit – string after stuffing : 0111110 ⇒ 0101 (Stuffed bit)
    ∴ Input string is 0111110101

    Correct Option: B

    Output bit – string after stuffing : 0111110 ⇒ 0101 (Stuffed bit)
    ∴ Input string is 0111110101

  1. A message is made up entirely of characters from the set X = {P,Q,R,S,T}. The table of probabilities for each of the characters is shown below:
    Character Probability
    P0.22
    Q0.34
    R0.17
    S0.19
    T0.08
    Total 1.00

    If a message of 100 characters over X is encoded using Huffman coding, then the expected length of the encoded message in bits is ________.








  1. View Hint View Answer Discuss in Forum

    By using haffman tree :

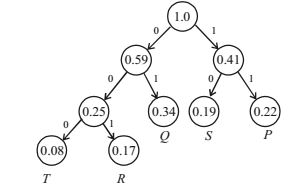
    So, number of bit required for each alphabet:
    T = 3 bit, R = 3 bit, Q = 2 bit, S = 2 bit, P = 2 bit
    Then, average length per character is = (number of bits * frequency of occurance of each alphabets)
    = 3 * 0.08 + 3 * 0.17 + 2 * 0.34 + 2 * 0.19 + 2 * 0.22 = 2.25 bits
    And, average length for 100 character = 2.25 * 100 = 225 bits.
    Hence, 225 bits is correct answer

    Correct Option: B

    By using haffman tree :

    So, number of bit required for each alphabet:
    T = 3 bit, R = 3 bit, Q = 2 bit, S = 2 bit, P = 2 bit
    Then, average length per character is = (number of bits * frequency of occurance of each alphabets)
    = 3 * 0.08 + 3 * 0.17 + 2 * 0.34 + 2 * 0.19 + 2 * 0.22 = 2.25 bits
    And, average length for 100 character = 2.25 * 100 = 225 bits.
    Hence, 225 bits is correct answer

  1. Consider two hosts X and Y, connected by a single direct link of rate 106 bits/sec. The distance between the two hosts is 10,000 km and the propagation speed along the link is 2 × 108 m/sec. Host X sends a file of 50,000 bytes as one large message to host Y continuously. Let the transmission and propagation delays be p milliseconds and q milliseconds, respectively. Then the values of p and q are








  1. View Hint View Answer Discuss in Forum

    As given that B (Bandwidth) = 106 bits/sec
    D (Distance) = 10,000 Km = 104 × 103 m = 107 m
    V (Velocity) = 2 × 108 m/s
    L(Data size) = 50,000 bytes = 50000 × 8 bits

    Transmission time (P) =
    Data size
    Bandwidth

    =
    50000 × 8 bits
    106 bits / sec

    P = 400 m / sec
    Propagation time (V) =
    Distance
    Velocity

    =
    10000 × 103 m
    2 × 108 m / sec

    = 50 × 105 - 8
    = 50 × 10-3 sec
    (q = 50 m/sec.)
    Hence option (d) is correct.

    Correct Option: D

    As given that B (Bandwidth) = 106 bits/sec
    D (Distance) = 10,000 Km = 104 × 103 m = 107 m
    V (Velocity) = 2 × 108 m/s
    L(Data size) = 50,000 bytes = 50000 × 8 bits

    Transmission time (P) =
    Data size
    Bandwidth

    =
    50000 × 8 bits
    106 bits / sec

    P = 400 m / sec
    Propagation time (V) =
    Distance
    Velocity

    =
    10000 × 103 m
    2 × 108 m / sec

    = 50 × 105 - 8
    = 50 × 10-3 sec
    (q = 50 m/sec.)
    Hence option (d) is correct.

  1. Consider a binary code that consists of only four valid codewords as given below :
    00000,01011,10101,11110
    Let the minimum Hamming distance of the code be p and the maximum number of erroneous bits that can be corrected by the code be q. Then the values of p and q are








  1. View Hint View Answer Discuss in Forum

    As given that Code = 00000, 01011, 10101, 11110
    Let Code 1 is 0 0 0 0 0
    Code 2 is 0 1 0 1 1
    Code 3 is 1 0 1 0 1
    Code 4 is 1 1 1 1 0
    Then the hamming distance between code 1 and code 2 is (3), because only three different digit between two code.
    Similarly: hamming distance between (Code 1 and Code 3), (Code 1 and Code 4), (Code 2 and Code 3), (Code 2 and Code 4), (Code 3 and Code 4) are 3, 4, 4, 3, 3 respectively. So, as per given data, minimum hamming distance of all code words is (P) considered as hamming distance is = 3, (P = 3).
    Now, the maximum number of erroneous bits that can be corrected (Code q), by the Hamming Code is = (2q + 1).
    According to hamming code,
    Minimum hamming distance of all the code word equal to the Maximum number of erroneous bits that can be corrected by the hamming code is
    3 = (2q + 1)
    3 – 1 = 2q

    q =
    2
    		 = 1
    2

    q = 1
    Hence, option (a) is correct.

    Correct Option: B

    As given that Code = 00000, 01011, 10101, 11110
    Let Code 1 is 0 0 0 0 0
    Code 2 is 0 1 0 1 1
    Code 3 is 1 0 1 0 1
    Code 4 is 1 1 1 1 0
    Then the hamming distance between code 1 and code 2 is (3), because only three different digit between two code.
    Similarly: hamming distance between (Code 1 and Code 3), (Code 1 and Code 4), (Code 2 and Code 3), (Code 2 and Code 4), (Code 3 and Code 4) are 3, 4, 4, 3, 3 respectively. So, as per given data, minimum hamming distance of all code words is (P) considered as hamming distance is = 3, (P = 3).
    Now, the maximum number of erroneous bits that can be corrected (Code q), by the Hamming Code is = (2q + 1).
    According to hamming code,
    Minimum hamming distance of all the code word equal to the Maximum number of erroneous bits that can be corrected by the hamming code is
    3 = (2q + 1)
    3 – 1 = 2q

    q =
    2
    		 = 1
    2

    q = 1
    Hence, option (a) is correct.