Computer networks miscellaneous
- A message is made up entirely of characters from the set X = {P,Q,R,S,T}. The table of probabilities for each of the characters is shown below:
Character Probability P 0.22 Q 0.34 R 0.17 S 0.19 T 0.08 Total 1.00
If a message of 100 characters over X is encoded using Huffman coding, then the expected length of the encoded message in bits is ________.
-
View Hint View Answer Discuss in Forum
By using haffman tree :
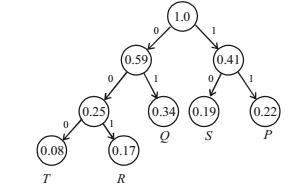
So, number of bit required for each alphabet:
T = 3 bit, R = 3 bit, Q = 2 bit, S = 2 bit, P = 2 bit
Then, average length per character is = (number of bits * frequency of occurance of each alphabets)
= 3 * 0.08 + 3 * 0.17 + 2 * 0.34 + 2 * 0.19 + 2 * 0.22 = 2.25 bits
And, average length for 100 character = 2.25 * 100 = 225 bits.
Hence, 225 bits is correct answerCorrect Option: B
By using haffman tree :

So, number of bit required for each alphabet:
T = 3 bit, R = 3 bit, Q = 2 bit, S = 2 bit, P = 2 bit
Then, average length per character is = (number of bits * frequency of occurance of each alphabets)
= 3 * 0.08 + 3 * 0.17 + 2 * 0.34 + 2 * 0.19 + 2 * 0.22 = 2.25 bits
And, average length for 100 character = 2.25 * 100 = 225 bits.
Hence, 225 bits is correct answer
- In a RSA cryptosystem, a participant A uses two prime numbers p = 13 and q =17 to generate her public and private keys. If the public key of A is 35, then the private key of A is ________.
-
View Hint View Answer Discuss in Forum
As given data P = 13, q = 17, e = 35, d = ?
As per RSA Algorithm.
n = P × q = 13 × 17 = 221
By using RSA formula ,
φ(n) = (P – 1) (q – 1) = 12 × 16 = 192.
To find out the private key of A, then take Modulas operater for RSA formula.
(d × e) mod φ(n) = 1
(d × 35) mod (192) = 1
d = 11, Hence, answer is 11.Correct Option: B
As given data P = 13, q = 17, e = 35, d = ?
As per RSA Algorithm.
n = P × q = 13 × 17 = 221
By using RSA formula ,
φ(n) = (P – 1) (q – 1) = 12 × 16 = 192.
To find out the private key of A, then take Modulas operater for RSA formula.
(d × e) mod φ(n) = 1
(d × 35) mod (192) = 1
d = 11, Hence, answer is 11.
- Consider a binary code that consists of only four valid codewords as given below :
00000,01011,10101,11110
Let the minimum Hamming distance of the code be p and the maximum number of erroneous bits that can be corrected by the code be q. Then the values of p and q are
-
View Hint View Answer Discuss in Forum
As given that Code = 00000, 01011, 10101, 11110
Let Code 1 is 0 0 0 0 0
Code 2 is 0 1 0 1 1
Code 3 is 1 0 1 0 1
Code 4 is 1 1 1 1 0
Then the hamming distance between code 1 and code 2 is (3), because only three different digit between two code.
Similarly: hamming distance between (Code 1 and Code 3), (Code 1 and Code 4), (Code 2 and Code 3), (Code 2 and Code 4), (Code 3 and Code 4) are 3, 4, 4, 3, 3 respectively. So, as per given data, minimum hamming distance of all code words is (P) considered as hamming distance is = 3, (P = 3).
Now, the maximum number of erroneous bits that can be corrected (Code q), by the Hamming Code is = (2q + 1).
According to hamming code,
Minimum hamming distance of all the code word equal to the Maximum number of erroneous bits that can be corrected by the hamming code is
3 = (2q + 1)
3 – 1 = 2qq = 2 = 1 2
q = 1
Hence, option (a) is correct.Correct Option: B
As given that Code = 00000, 01011, 10101, 11110
Let Code 1 is 0 0 0 0 0
Code 2 is 0 1 0 1 1
Code 3 is 1 0 1 0 1
Code 4 is 1 1 1 1 0
Then the hamming distance between code 1 and code 2 is (3), because only three different digit between two code.
Similarly: hamming distance between (Code 1 and Code 3), (Code 1 and Code 4), (Code 2 and Code 3), (Code 2 and Code 4), (Code 3 and Code 4) are 3, 4, 4, 3, 3 respectively. So, as per given data, minimum hamming distance of all code words is (P) considered as hamming distance is = 3, (P = 3).
Now, the maximum number of erroneous bits that can be corrected (Code q), by the Hamming Code is = (2q + 1).
According to hamming code,
Minimum hamming distance of all the code word equal to the Maximum number of erroneous bits that can be corrected by the hamming code is
3 = (2q + 1)
3 – 1 = 2qq = 2 = 1 2
q = 1
Hence, option (a) is correct.
- Consider two hosts X and Y, connected by a single direct link of rate 106 bits/sec. The distance between the two hosts is 10,000 km and the propagation speed along the link is 2 × 108 m/sec. Host X sends a file of 50,000 bytes as one large message to host Y continuously. Let the transmission and propagation delays be p milliseconds and q milliseconds, respectively. Then the values of p and q are
-
View Hint View Answer Discuss in Forum
As given that B (Bandwidth) = 106 bits/sec
D (Distance) = 10,000 Km = 104 × 103 m = 107 m
V (Velocity) = 2 × 108 m/s
L(Data size) = 50,000 bytes = 50000 × 8 bitsTransmission time (P) = Data size Bandwidth = 50000 × 8 bits 106 bits / sec
P = 400 m / secPropagation time (V) = Distance Velocity = 10000 × 103 m 2 × 108 m / sec
= 50 × 105 - 8
= 50 × 10-3 sec
(q = 50 m/sec.)
Hence option (d) is correct.Correct Option: D
As given that B (Bandwidth) = 106 bits/sec
D (Distance) = 10,000 Km = 104 × 103 m = 107 m
V (Velocity) = 2 × 108 m/s
L(Data size) = 50,000 bytes = 50000 × 8 bitsTransmission time (P) = Data size Bandwidth = 50000 × 8 bits 106 bits / sec
P = 400 m / secPropagation time (V) = Distance Velocity = 10000 × 103 m 2 × 108 m / sec
= 50 × 105 - 8
= 50 × 10-3 sec
(q = 50 m/sec.)
Hence option (d) is correct.
- Which of the following functionalities must be implemented by a transport protocol over and above the network protocol?
-
View Hint View Answer Discuss in Forum
The transport layer of TCP/IP model is very similar to the transport layer of OSI model. The transport layer is more commonly known as Host to Host protocol layer as it is responsible to setup and maintain (end to end communication) between two hosts. Hence, the transport protocols maintain the end to end connectivity.
Correct Option: D
The transport layer of TCP/IP model is very similar to the transport layer of OSI model. The transport layer is more commonly known as Host to Host protocol layer as it is responsible to setup and maintain (end to end communication) between two hosts. Hence, the transport protocols maintain the end to end connectivity.

