Computer networks miscellaneous
- Consider a binary code that consists of only four valid codewords as given below :
00000,01011,10101,11110
Let the minimum Hamming distance of the code be p and the maximum number of erroneous bits that can be corrected by the code be q. Then the values of p and q are
-
View Hint View Answer Discuss in Forum
As given that Code = 00000, 01011, 10101, 11110
Let Code 1 is 0 0 0 0 0
Code 2 is 0 1 0 1 1
Code 3 is 1 0 1 0 1
Code 4 is 1 1 1 1 0
Then the hamming distance between code 1 and code 2 is (3), because only three different digit between two code.
Similarly: hamming distance between (Code 1 and Code 3), (Code 1 and Code 4), (Code 2 and Code 3), (Code 2 and Code 4), (Code 3 and Code 4) are 3, 4, 4, 3, 3 respectively. So, as per given data, minimum hamming distance of all code words is (P) considered as hamming distance is = 3, (P = 3).
Now, the maximum number of erroneous bits that can be corrected (Code q), by the Hamming Code is = (2q + 1).
According to hamming code,
Minimum hamming distance of all the code word equal to the Maximum number of erroneous bits that can be corrected by the hamming code is
3 = (2q + 1)
3 – 1 = 2qq = 2 = 1 2
q = 1
Hence, option (a) is correct.Correct Option: B
As given that Code = 00000, 01011, 10101, 11110
Let Code 1 is 0 0 0 0 0
Code 2 is 0 1 0 1 1
Code 3 is 1 0 1 0 1
Code 4 is 1 1 1 1 0
Then the hamming distance between code 1 and code 2 is (3), because only three different digit between two code.
Similarly: hamming distance between (Code 1 and Code 3), (Code 1 and Code 4), (Code 2 and Code 3), (Code 2 and Code 4), (Code 3 and Code 4) are 3, 4, 4, 3, 3 respectively. So, as per given data, minimum hamming distance of all code words is (P) considered as hamming distance is = 3, (P = 3).
Now, the maximum number of erroneous bits that can be corrected (Code q), by the Hamming Code is = (2q + 1).
According to hamming code,
Minimum hamming distance of all the code word equal to the Maximum number of erroneous bits that can be corrected by the hamming code is
3 = (2q + 1)
3 – 1 = 2qq = 2 = 1 2
q = 1
Hence, option (a) is correct.
- In a RSA cryptosystem, a participant A uses two prime numbers p = 13 and q =17 to generate her public and private keys. If the public key of A is 35, then the private key of A is ________.
-
View Hint View Answer Discuss in Forum
As given data P = 13, q = 17, e = 35, d = ?
As per RSA Algorithm.
n = P × q = 13 × 17 = 221
By using RSA formula ,
φ(n) = (P – 1) (q – 1) = 12 × 16 = 192.
To find out the private key of A, then take Modulas operater for RSA formula.
(d × e) mod φ(n) = 1
(d × 35) mod (192) = 1
d = 11, Hence, answer is 11.Correct Option: B
As given data P = 13, q = 17, e = 35, d = ?
As per RSA Algorithm.
n = P × q = 13 × 17 = 221
By using RSA formula ,
φ(n) = (P – 1) (q – 1) = 12 × 16 = 192.
To find out the private key of A, then take Modulas operater for RSA formula.
(d × e) mod φ(n) = 1
(d × 35) mod (192) = 1
d = 11, Hence, answer is 11.
- Consider the different activities related to email :
m1 : Send an email from a mail client to a mail server.
m2 : Download an email from mailbox server to a mail client.
m3 : Checking email in a web browser.
Which is the application level protocol used in each activity?
-
View Hint View Answer Discuss in Forum
Sending an email will be done through user agent and message transfer agent by SMTP, downloading an email from mail box is done through POP, checking email in a web browser is done through HTTP.
Correct Option: C
Sending an email will be done through user agent and message transfer agent by SMTP, downloading an email from mail box is done through POP, checking email in a web browser is done through HTTP.
- A computer network uses polynomials over GF(2) for error checking with 8 bits as information bits and uses x 3 + x + 1 as the generator polynomial to generate the check bits. In this network, the message 01011011 is transmitted as
-
View Hint View Answer Discuss in Forum
The given generator polynomial (LRC)
G(X) = X3 + X + 1
⇒ 1.X3 + 0.X2 + 1.X1 + 1.X0
G(X) ⇒ 1 0 1 1
Given message m(X) = 0 1 0 1 1 0 1 1.
Then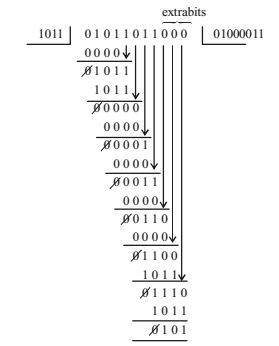
So, the message 01011011 is transmitted as 01011011101. So, option (c) is correct.Correct Option: C
The given generator polynomial (LRC)
G(X) = X3 + X + 1
⇒ 1.X3 + 0.X2 + 1.X1 + 1.X0
G(X) ⇒ 1 0 1 1
Given message m(X) = 0 1 0 1 1 0 1 1.
Then
So, the message 01011011 is transmitted as 01011011101. So, option (c) is correct.
- A link has a transmission speed of 106 bits/sec. It uses data packets of size 1000 bytes each. Assume that the acknowledgement has negligible transmission delay, and that its propagation delay is the same as the data propagation delay. Also assume that the processing delays at nodes are negligible. The efficiency of the stop-and-wait protocol in this setup is exactly 25%. The value of the oneway propagation delay(in milliseconds) is _______.
-
View Hint View Answer Discuss in Forum
Given, B = 106 bps
L = 1000 bytes
h = 25%
Tp = ?In stop-and-wait, η = 1 1 + 2a ⇒ 1 = 1 = 1 + 2a = 4 4 1 + 2a 2a = 3 ; a = 3 2 Tx = L = 8 × 103 = 8 ms B 106 Tp = 3 ; 2Tp = 3T Tx 2
2Tp = 24 ms
Tp = 12 ms
Correct Option: B
Given, B = 106 bps
L = 1000 bytes
h = 25%
Tp = ?In stop-and-wait, η = 1 1 + 2a ⇒ 1 = 1 = 1 + 2a = 4 4 1 + 2a 2a = 3 ; a = 3 2 Tx = L = 8 × 103 = 8 ms B 106 Tp = 3 ; 2Tp = 3T Tx 2
2Tp = 24 ms
Tp = 12 ms

