Architecture and Planning Miscellaneous-topic

Architecture and Planning Miscellaneous-topic

Easy Questions
Moderate Questions
Difficult Questions

Architecture and Planning Miscellaneous

Architecture and Planning Miscellaneous-topic
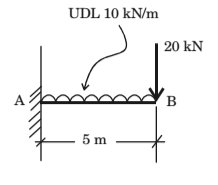
  1. In the Figure, the negative bending moment at point A of the cantilever is ________ kNm.









  1. View Hint View Answer Discuss in Forum

    224 to 226
    For a contilever beam lengt h ‘L’ carrying a concentrated load ‘W’ at its fixend, B. M.max = – (WL)
    Here, due to point load B. M.max = (– WL) = (– 20 × 5) = – 100 kN.m.
    For a contilever beam of length ‘L’ carrying on UDL ‘w’ over its entire spar B. M.max at fixed end = (WL²/2)
    Here, due to UDLB, M.max = (WL²/2)

    (- 10 × 5²)
    		 = - 125 kN.m.
    2

    Thus, total B.M. moment at point A (fixed end) = – 100 + (– 125) = – 225 kN.m.

    Correct Option: D

    224 to 226
    For a contilever beam lengt h ‘L’ carrying a concentrated load ‘W’ at its fixend, B. M.max = – (WL)
    Here, due to point load B. M.max = (– WL) = (– 20 × 5) = – 100 kN.m.
    For a contilever beam of length ‘L’ carrying on UDL ‘w’ over its entire spar B. M.max at fixed end = (WL²/2)
    Here, due to UDLB, M.max = (WL²/2)

    (- 10 × 5²)
    		 = - 125 kN.m.
    2

    Thus, total B.M. moment at point A (fixed end) = – 100 + (– 125) = – 225 kN.m.

  1. For an activity, ‘optimistic time duration’ is 4 days, ‘pessimistic time duration’ is 11 days and ‘mostlikely time duration’ is 8 days. The PERT value of time duration is______ days (up to one decimal place).








  1. View Hint View Answer Discuss in Forum

    7.8 to 7.9
    PERT value of time duration/Expected time (te)

    =
    (t0 + 4tm + t0)
    6

    Where, to = Optimistic time, tm = Most likely time, tp = Pessimistic time.
    Thus, (te) =
    (t0 + 4tm + t0)
    6

    =
    {(4 + (4 × 8) + 11}
    		 = 7.83 days.
    6

    Correct Option: A

    7.8 to 7.9
    PERT value of time duration/Expected time (te)

    =
    (t0 + 4tm + t0)
    6

    Where, to = Optimistic time, tm = Most likely time, tp = Pessimistic time.
    Thus, (te) =
    (t0 + 4tm + t0)
    6

    =
    {(4 + (4 × 8) + 11}
    		 = 7.83 days.
    6

  1. A 5m × 5m × 3m room has four 230 mm thick external brick walls. Total wall fenestration is 10 sqm. The temperature difference between indoor and outdoor is 2 degC. The air to air transmittance values for 230 mm thick brick wall and 200 mm thick aerated concrete block wall are 2.4 and 1.7 W/sqm degC respectively. If the brick walls are replaced with the aerated concrete block walls, then the change in conductive heat flow through the walls is _________W.








  1. View Hint View Answer Discuss in Forum

    69.5 to 70.5
    Here, Area of 4 walls of the room = 4 × (5 × 3) = 60 m², Height = 3m.
    Total area of wall fenestration (Openings) = 10 m².
    Thus, net external wall area= 50 m²
    Thermal transmittance value of 230 mm thick brick wall (U-value of wall) = 2.4 W/sq.m. deg C.
    Thermal transmittance value of 200 mm thick aerated concrete block wall (U-value of aerated concrete wall) 1.7 W/sq.m. deg C
    Difference between out door and indoor temperature (At) = 2°
    Conductive heat flow through brick wall
    = (U-value of brick wall × area of wall × Δt) = (2.4 × 50 × 2) = 240 watts. Conductive heat flow through aerated concrete block wall = (U-value of ACC wall x area of wall × Δt) = (1.7 × 50 × 2) = 170 watts.
    Thus, change in conductive heat flow through the wall due to change of materials = 240 – 170 = 70 Watts.

    Correct Option: C

    69.5 to 70.5
    Here, Area of 4 walls of the room = 4 × (5 × 3) = 60 m², Height = 3m.
    Total area of wall fenestration (Openings) = 10 m².
    Thus, net external wall area= 50 m²
    Thermal transmittance value of 230 mm thick brick wall (U-value of wall) = 2.4 W/sq.m. deg C.
    Thermal transmittance value of 200 mm thick aerated concrete block wall (U-value of aerated concrete wall) 1.7 W/sq.m. deg C
    Difference between out door and indoor temperature (At) = 2°
    Conductive heat flow through brick wall
    = (U-value of brick wall × area of wall × Δt) = (2.4 × 50 × 2) = 240 watts. Conductive heat flow through aerated concrete block wall = (U-value of ACC wall x area of wall × Δt) = (1.7 × 50 × 2) = 170 watts.
    Thus, change in conductive heat flow through the wall due to change of materials = 240 – 170 = 70 Watts.

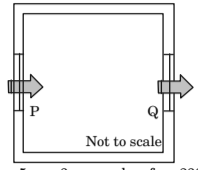
  1. An isolated enclosure shown in the Figure has inlet P and outlet Q of 2 sqm each, on the opposite walls. The outdoor wind speed is 5 m/sec. If the coefficient of effectiveness is 0.6, the rate of natural ventilation in the enclosure due to wind action is _________ cum/hr.








  1. View Hint View Answer Discuss in Forum

    21600 to 21600
    Volume of air getting extracted from the Inlet/Outlet

    Area of
    Area of Inlet
    		 .(V = A × S)
    Outlet × Speed

    Here, The area of inlet and outlet = 2 sq.m, and wind speed = 5m/sec.
    Thus, volume of air getting extracted from inlet P per second = 2m² × 5m/sec = 10m³/sec.
    As we know, 1 hr. = 60 min = 3600 sec.
    Volume of air getting extracted inside from inlet P per hour = 10m³ × 3600/hr. = 36000 m³/hr.
    If the co-efficient of effect iveness is 1 then, amount of air getting extracted frominlet = amount of air extracted from outlet.
    Here, co-efficient of effectiveness = 0.6
    Thus, rate of natural ventilation per hour = 0.6 × amount of air coming inside from inlet P per hour = 0.6 × 36,000 = 21,600 m³/hour.

    Correct Option: A

    21600 to 21600
    Volume of air getting extracted from the Inlet/Outlet

    Area of
    Area of Inlet
    		 .(V = A × S)
    Outlet × Speed

    Here, The area of inlet and outlet = 2 sq.m, and wind speed = 5m/sec.
    Thus, volume of air getting extracted from inlet P per second = 2m² × 5m/sec = 10m³/sec.
    As we know, 1 hr. = 60 min = 3600 sec.
    Volume of air getting extracted inside from inlet P per hour = 10m³ × 3600/hr. = 36000 m³/hr.
    If the co-efficient of effect iveness is 1 then, amount of air getting extracted frominlet = amount of air extracted from outlet.
    Here, co-efficient of effectiveness = 0.6
    Thus, rate of natural ventilation per hour = 0.6 × amount of air coming inside from inlet P per hour = 0.6 × 36,000 = 21,600 m³/hour.

  1. In a mixed use development on a 2.0 hectare site with 2.0 FAR, the ratio of residential to commercial floor area is 3:2. The minimum parking (in ECS) needed per 100 sqm of residential and commercial floor area is 1.0 and 1.25 respectively. Considering fullFAR utilization, the total par king requirement is ____________ ECS.








  1. View Hint View Answer Discuss in Forum

    440 to 440
    Site Area = 2.0 hectare = 20,000 sq.m. Maximum
    FAR = 2.0. Thus, Maximum Built-up Area = 40,000 sq.m.
    It is given that, Ratio of residential: commercial floor area = 3: 2
    Thus, Area for residential as per 3: 2 ratio = 24,000 sq.m. & Area for commercial as per 3: 2 ratio = 16,000 sq.m.
    Minimum parking (in ECS) needed per 100 sq.m, of residential area = 1.
    Thus, ECS required for 24,000 sq.m, of residential area = 240
    Minimum parking (in ECS) needed per 100 sq.m, of commercial area = 1.25.
    Thus, ECS required for 16,000 sq.m, of commercial area = 200
    Thus, total ECS required for 40,000 sq.m, of maximum built-up area = 240 + 200 = 440

    Correct Option: A

    440 to 440
    Site Area = 2.0 hectare = 20,000 sq.m. Maximum
    FAR = 2.0. Thus, Maximum Built-up Area = 40,000 sq.m.
    It is given that, Ratio of residential: commercial floor area = 3: 2
    Thus, Area for residential as per 3: 2 ratio = 24,000 sq.m. & Area for commercial as per 3: 2 ratio = 16,000 sq.m.
    Minimum parking (in ECS) needed per 100 sq.m, of residential area = 1.
    Thus, ECS required for 24,000 sq.m, of residential area = 240
    Minimum parking (in ECS) needed per 100 sq.m, of commercial area = 1.25.
    Thus, ECS required for 16,000 sq.m, of commercial area = 200
    Thus, total ECS required for 40,000 sq.m, of maximum built-up area = 240 + 200 = 440