26. The period of the output waveform for the circuit of figure shown, when triggered by a negative pulse is
    
    

1. 1. 0.75 ms

   
   
   

   2. 0.825 ms

   
   
   

   3. 0.525 ms

   
   
   

   4. 1.5 ms

   
   
   

---

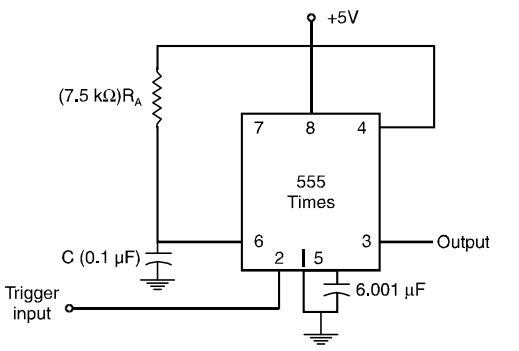
1. View Hint View Answer Discuss in Forum

   T = (1.1) R_AC
   = 1.1(7.5 × 10³) (0.1 × 10^{– 6}) = 0.825 ms.

   Correct Option: B

   T = (1.1) R_AC
   = 1.1(7.5 × 10³) (0.1 × 10^{– 6}) = 0.825 ms.

---

27. What is the hysterisis voltage of the submitt trigger shown if V_sat = ± 10V ?
    
    

1. 1. 1.90 volts

   
   
   

   2. 1.45 volts

   
   
   

   3. 1.00 volt

   
   
   

   4. 0.90 volt

   
   
   

---

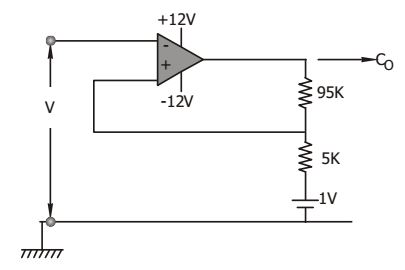
1. View Hint View Answer Discuss in Forum

   Hysterisis voltage,
   

   VH =	2 R2 V0	=	2 × 5 × 10	= 1 volt
   	R1 + R2		100

   
   

   Correct Option: C

   Hysterisis voltage,
   

   VH =	2 R2 V0	=	2 × 5 × 10	= 1 volt
   	R1 + R2		100

   
   

---

---

28. In the circuit of shown in the figure, LED will be ON if v_i is
    
    

1. 1. > 10 V

   
   
   

   2. < 10 V

   
   
   

   3. > 5 V

   
   
   

   4. < 5 V

   
   
   

---

1. View Hint View Answer Discuss in Forum

   υ_ =	(10)(10k)	= 5 V
   	10k + 10k

   
   When υ₊ > 5 V, output will be positive and LED will be ON Hence (c) is correct answer.

   Correct Option: C

   υ_ =	(10)(10k)	= 5 V
   	10k + 10k

   
   When υ₊ > 5 V, output will be positive and LED will be ON Hence (c) is correct answer.

---

29. For the circuit of the given figure with an ideal operational amplifier, maximum phase shift of the output V_out with reference to the input V_in is
    

1. 1. 0°

   
   
   

   2. – 90°

   
   
   

   3. + 90°

   
   
   

   4. + 180°

   
   
   

---

1. View Hint View Answer Discuss in Forum

   From the circuit,
   

   V+ =	Vin
   	1 + jωRC

   
   and V_– =V₊ (Ideal OPAMP) Now
   

   Now	Vin - V–	=	V– – V0
   	R1		R1

   
   ⇒ V₀ = 2V_– – V_in = 2V₊ – V_in
   

   =		2	- 1		Vin =	1 - jωRC	V0
   		1 + jωRC				1 + jωRC

   
   ∴ ∠ (V₀ / V_i) = - 2 tan^-1 ωRC
   For – 90 ≤ θ ≤ 90°
   Phase-shift ∠ (V₀ / V_i) = ± 180°
   

   Correct Option: D

   From the circuit,
   

   V+ =	Vin
   	1 + jωRC

   
   and V_– =V₊ (Ideal OPAMP) Now
   

   Now	Vin - V–	=	V– – V0
   	R1		R1

   
   ⇒ V₀ = 2V_– – V_in = 2V₊ – V_in
   

   =		2	- 1		Vin =	1 - jωRC	V0
   		1 + jωRC				1 + jωRC

   
   ∴ ∠ (V₀ / V_i) = - 2 tan^-1 ωRC
   For – 90 ≤ θ ≤ 90°
   Phase-shift ∠ (V₀ / V_i) = ± 180°
   

---

---

30. Assuming operational amplifier to be ideal, gain V_out / V_in for the circuit shown in the given figure is
    
    

1. 1. – 1

   
   
   

   2. – 20

   
   
   

   3. – 100

   
   
   

   4. – 120

   
   
   

---

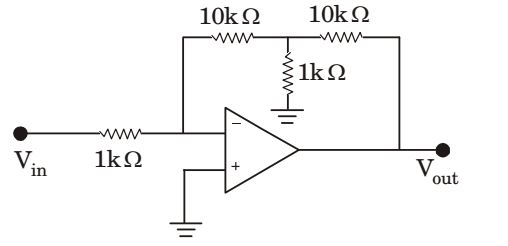
1. View Hint View Answer Discuss in Forum

   
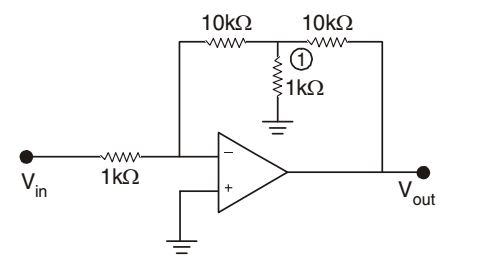
   Using KCL at the node 1 we have
   

   	V - 0	+	V	+	V - Vout	= 0
   	10		1		10

   
   ⇒ 12V = V_out ...(i)
   Also, using KCL at inverting node, we get
   

   	Vin - 0	=	0 – V
   	1		10

   
   ⇒ V = – V_in. 10 ...(ii)
   From equations (i) and (ii), we get
   

   	Vout	= -120
   	Vin

   
   

   Correct Option: D

   
   Using KCL at the node 1 we have
   

   	V - 0	+	V	+	V - Vout	= 0
   	10		1		10

   
   ⇒ 12V = V_out ...(i)
   Also, using KCL at inverting node, we get
   

   	Vin - 0	=	0 – V
   	1		10

   
   ⇒ V = – V_in. 10 ...(ii)
   From equations (i) and (ii), we get
   

   	Vout	= -120
   	Vin

   
   

---