Analog circuits miscellaneous
- In the given circuit the silicon transistor has β = 75 collector voltage VC = 9V. The ratio of RB and RC is ______.

-
View Hint View Answer Discuss in Forum
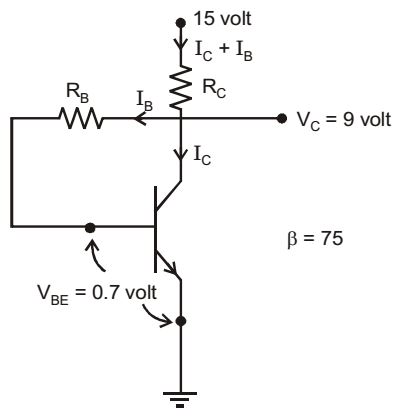
IC = BIB
IC = 75 IB
IC + IB = 75 IB + IB = 76IBIC + IB = 15 - 9 RC 76 IB = 6 ...(i) RC IB = 9 - 0.7 = 8.3 ...(ii) RB RB
Equation (i) / Equation (ii),76IB = 6 / RC = 6 × RB IB 8.3 / RC RC 8.3 RB = 76 × 8.3 = 105.1 RC 6 RB = 105.13 RC
Correct Option: B

IC = BIB
IC = 75 IB
IC + IB = 75 IB + IB = 76IBIC + IB = 15 - 9 RC 76 IB = 6 ...(i) RC IB = 9 - 0.7 = 8.3 ...(ii) RB RB
Equation (i) / Equation (ii),76IB = 6 / RC = 6 × RB IB 8.3 / RC RC 8.3 RB = 76 × 8.3 = 105.1 RC 6 RB = 105.13 RC
- Two perfectly matched silicon transistors are connected as shown in the figure. Assuming the β of the transistors to be very high and the forward voltage drop in diodes to be 0.7 V, the value of current I is
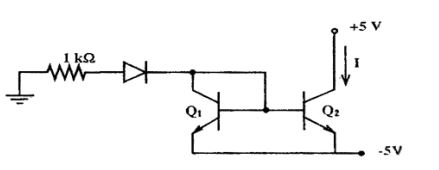
-
View Hint View Answer Discuss in Forum
Since Both thyristor are perfectly matched, so VBE1 = VBE2
∴ IC1 = exp 
VBE1 - VBE2 
= e0 = 1 IC2 VT
Since β for both are same, therefore IB1 = IB2 = IB
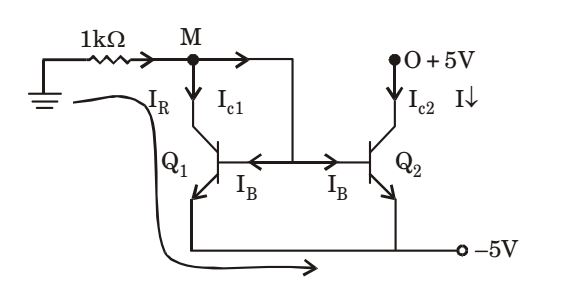
Now by KVL in loop as shown,IR = 0 - 0.7 - (-5) = 4.3 mA 1 kΩ
By KCL at point M
IR = IC1 + 2 IBIR = IC1 + 2 IC1 β ∴ IC1 = β IR β + 2 For large β , β ≈ 1 β + 2
∴ IC1 = IR = 4.3 mA
∴ I = IC2 = IC1 = 4.3 mA
Correct Option: C
Since Both thyristor are perfectly matched, so VBE1 = VBE2

∴ IC1 = exp 
VBE1 - VBE2 
= e0 = 1 IC2 VT
Since β for both are same, therefore IB1 = IB2 = IB
Now by KVL in loop as shown,IR = 0 - 0.7 - (-5) = 4.3 mA 1 kΩ
By KCL at point M
IR = IC1 + 2 IBIR = IC1 + 2 IC1 β ∴ IC1 = β IR β + 2 For large β , β ≈ 1 β + 2
∴ IC1 = IR = 4.3 mA
∴ I = IC2 = IC1 = 4.3 mA
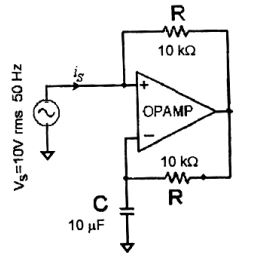
- The following circuit has R = 10k&ohm:, C = 10&m;F. The input voltage is a sinusoid at 50Hz with an rms value of 10V under ideal conditions, the current is from the source is
-
View Hint View Answer Discuss in Forum
Xc = 1 = 1 = 103 ohm ω C 2π × 50 × 10μF π VA = - jXc . V0 -jXc + R ∴ V0 = - jXc + R . VA -jXc 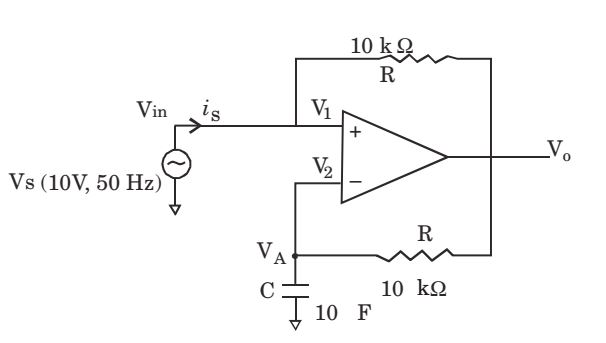
Assuming virtual ground,
Vin = VA = 10V∴ V0 = - jXc + R . 10 -jXc Current , is = Vin - V0 R = 1 
10 - -jXc + R .10 
104 -jXc = 1 
1 - -jXc + R 
103 -jXc = 1 
-jXc + jXc - R 
103 -jXc = 1 R = 1 . 1 × 10 × 103 103 jXc j 103 (103 / π) = 10π × 10-3 = (10π mA) ∠ -90° lagging j
Alternately
V1 = Vs = R . is + V0V2 = Vo 1 jωC = Vo 1 1 + R 1 + jωRC jωC But Vo = A(V1 – V2) = A 
Vs - V0 
1 + jωRC ⇒ Vo 
1 + A 
= AVs 1 + jωRC ⇒ V0 = A(1 + jωRC) ≃ 1 + jωRC Vs 1 + jωRC + A
= 1 + j 100 π × 104 × 10 × 10–6 = 1 + j 10π
⇒ Vo = Vs (1 + j 10π) = 10 (1 + j 10π)
But Vs = R . is + Voor is = Vs - V0 = 10 - 10 - j100π R 10 × 103
= – j 10π mA = 10π ∠– 90° mA
Correct Option: D
Xc = 1 = 1 = 103 ohm ω C 2π × 50 × 10μF π VA = - jXc . V0 -jXc + R ∴ V0 = - jXc + R . VA -jXc 
Assuming virtual ground,
Vin = VA = 10V∴ V0 = - jXc + R . 10 -jXc Current , is = Vin - V0 R = 1 
10 - -jXc + R .10 
104 -jXc = 1 
1 - -jXc + R 
103 -jXc = 1 
-jXc + jXc - R 
103 -jXc = 1 R = 1 . 1 × 10 × 103 103 jXc j 103 (103 / π) = 10π × 10-3 = (10π mA) ∠ -90° lagging j
Alternately
V1 = Vs = R . is + V0V2 = Vo 1 jωC = Vo 1 1 + R 1 + jωRC jωC But Vo = A(V1 – V2) = A 
Vs - V0 
1 + jωRC ⇒ Vo 
1 + A 
= AVs 1 + jωRC ⇒ V0 = A(1 + jωRC) ≃ 1 + jωRC Vs 1 + jωRC + A
= 1 + j 100 π × 104 × 10 × 10–6 = 1 + j 10π
⇒ Vo = Vs (1 + j 10π) = 10 (1 + j 10π)
But Vs = R . is + Voor is = Vs - V0 = 10 - 10 - j100π R 10 × 103
= – j 10π mA = 10π ∠– 90° mA
- For the circuit shown below,
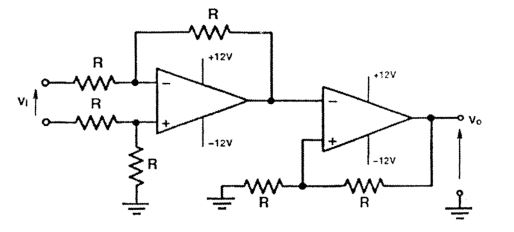
the CORRECT transfer characteristic is
-
View Hint View Answer Discuss in Forum
Redrawing the first stage,
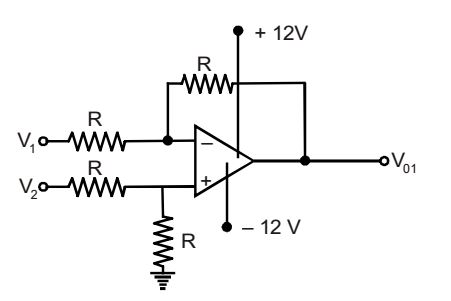
Assuming ideal OPAMP’sV- = V+ = V2 2 V+ = V2 R = V2 R + R 2
Using KCL at inverting terminal, we getV1 - V- = V- - V01 R R
⇒ V01 = 2V– – V1 = V2 – V1
= – Vi [as V1 – V2 = Vi]
For the second-stage schmitt-trigger.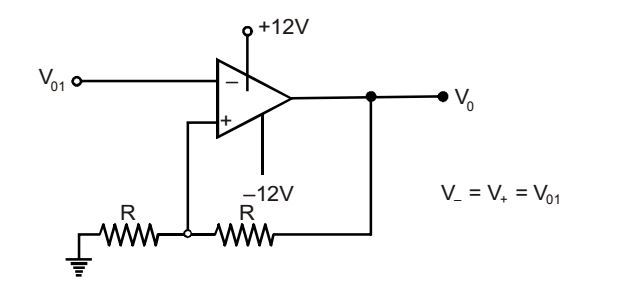
For V01 < V+ or Vi > V+, V0 = 12 Voltsv+ = R VR + R V0 ≡ V1 R + R R + R
As VR = 0 [VR is grounded]v+ = V0 ≡ V1 .......(A) 2
For v01 > v+
or vi < v+ , v0 = – 12 volts
The voltage at the non-inverting terminal is,v+ = R VR - R V0 ≡ V2 R + R R + R v+ = - V0 ≡ V2 2 
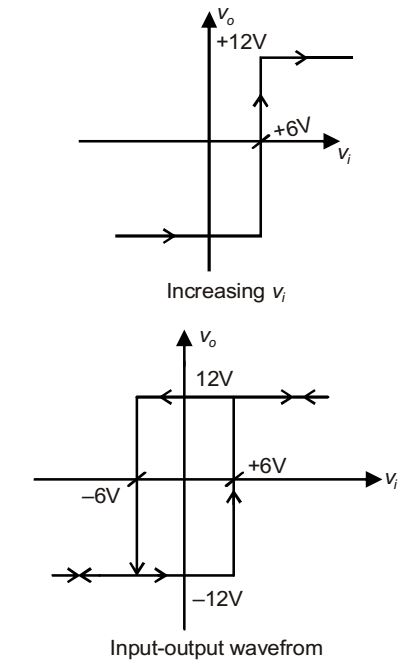
Correct Option: D
Redrawing the first stage,

Assuming ideal OPAMP’sV- = V+ = V2 2 V+ = V2 R = V2 R + R 2
Using KCL at inverting terminal, we getV1 - V- = V- - V01 R R
⇒ V01 = 2V– – V1 = V2 – V1
= – Vi [as V1 – V2 = Vi]
For the second-stage schmitt-trigger.
For V01 < V+ or Vi > V+, V0 = 12 Voltsv+ = R VR + R V0 ≡ V1 R + R R + R
As VR = 0 [VR is grounded]v+ = V0 ≡ V1 .......(A) 2
For v01 > v+
or vi < v+ , v0 = – 12 volts
The voltage at the non-inverting terminal is,v+ = R VR - R V0 ≡ V2 R + R R + R v+ = - V0 ≡ V2 2 

- Given that the op-amps in the figure are ideal, the output voltage V0 is
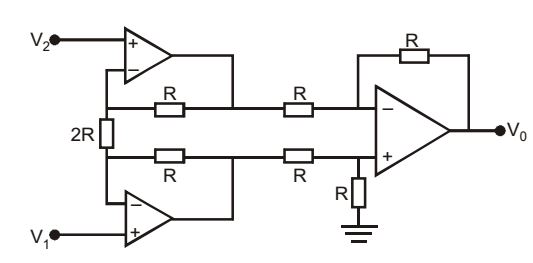
-
View Hint View Answer Discuss in Forum
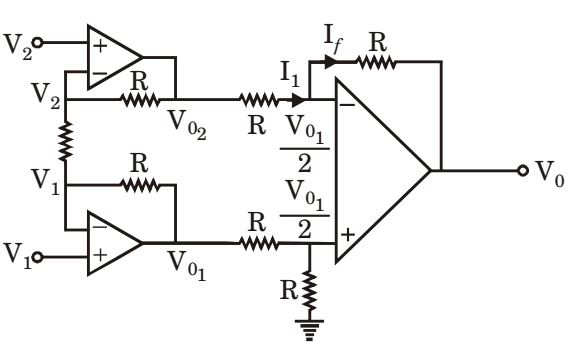
V2 - V1 + V2 - V02 = 0 2R R ∴ V02 = 3V2 - V1 .....(i) 2
V1 - V2 + V1 - V01 = 0 2R R ∴ V01 = 3V1 - V2 ......(ii) 2
∵ I1 = If
V02 - V01 
= 
V01 - V0 
2 2 R R
From equation (i) and (ii)
∴ V0 = V01 – V02= 
3V1 - V2 
- 
3V2 - V1 
2 2
V0 = 2(V1 – V2)Correct Option: B

V2 - V1 + V2 - V02 = 0 2R R ∴ V02 = 3V2 - V1 .....(i) 2
V1 - V2 + V1 - V01 = 0 2R R ∴ V01 = 3V1 - V2 ......(ii) 2
∵ I1 = If
V02 - V01 
= 
V01 - V0 
2 2 R R
From equation (i) and (ii)
∴ V0 = V01 – V02= 
3V1 - V2 
- 
3V2 - V1 
2 2
V0 = 2(V1 – V2)

