Cubes and Dices
The questions based on cubes, test the ability of the students to visualize and deal with the multidimensional problems/ situations.
Cube
A three dimensional figure having 6 square faces, 8 vertices and 12 edges with equal length, breadth and height is called cube.
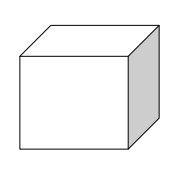
In a cube:
Number of vertices V = 8
Number of Faces F = 6
Number of Edges E = 12
We know that
| Euler’s formula = F + V = E + 2 |
Cuboid
A three dimensional figure in which length, breadth and height are different.
In cuboid 6 rectangular faces, 8 vertices and 12 edges.
| Total number of small cubes = l × b × h |

Important Formula
| Total number of small cube = n³ |
Where n = Number of rows/columns
| 1 side colored small cubes = 6 (n - 2)² |
| 2 sides colored small cubes = 12 (n - 2)² |
| 3 sides colored small cubes = 8 |
| 4 sides colored small cubes = 0 |
| Colorless/Unseen cubes = (n - 2)³ |
Ex- A cube having dimension 5 cm has been transformed into smaller cube having dimension 1 cm. Then whole block is colored with pink color . Find
(1). Total number of small cubes
(2). 1 side colored small cubes
(3). 2 sides colored small cubes
(4). 3 sides colored small cubes
(5). 4 sides colored small cubes
(6). colorless cubes
Solution:- (1). Total number of small cubes = n3 = 53 = 125
(2). 1 side colored small cubes = 6(n - 2)2
= 6( 5 - 2 )2
= 6 × 32
= 6 × 9
= 54
(3). 2 sides colored small cubes = 12(n - 2)
= 12 ( 5 - 2 ) = 12 × 3 = 36
(4). 3 sides colored small cubes = 8
(5). 4 sides colored small cubes = 0
(6). Colorless cubes = ( n - 2 )3
= ( 5 - 2 )3 = 33 = 27
Direction: 216 cubes of similar size are arranged in the form of the bigger cube (6 cubes on each side, i.e.., 6 x 6 x 6) all the exposed surfaces are painted.
Ex- How many of the cubes have 0 faces painted?
(1) 64
(2) 125
(3) 27
(4) None of these
Solution:-Total number of cubes = n3
or, 216 = n3
∴ n = 6
Number of colorless cubes = ( n - 2 )3
Number of the cubes with 0 faces painted is = (6 - 2)3 = 43 = 64
• If we make a cut in one plane then we divide the cube in two parts (as shown in fig 1), if we make 2 cuts in same plane then we will get 2 + 1 = 3 pieces (as shown in fig 2) similarly if we make ‘p’ cuts in one plane then we will get ‘p + 1’ pieces as shown in Fig 3.
• If we make a cut in 2nd plane then we divide the cube in 2(p + 1) parts (as shown in fig 4), if we make 2 cuts in same plane then we will get (2 + 1) (p + 1) pieces (as shown in fig 5) similarly if we make ‘q’ cuts in 2nd plane then we will get ‘(p + 1) (q + 1) ’ pieces as shown in Fig 6.

• If we make a cut in 3rd plane then we divide the cube in 2(p + 1) (q + 1) parts (as shown in fig 7), if we make 2 cuts in same plane then we will get (2 + 1) (p + 1) (q + 1) pieces (as shown in fig 8) similarly if we make ‘q’ cuts in 3rd plane then we will get ‘(p + 1) (q + 1) (r + 1) ’ pieces as shown in Fig 9.
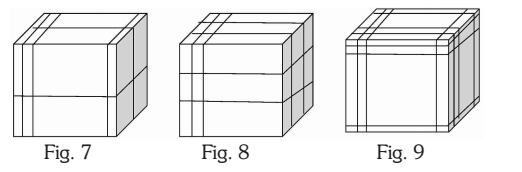
Note: ‘a’ Number of cuts in one plane gives (a + 1) pieces, while ‘b’ cuts in another plane gives (b + 1) pieces, and ‘c’ cuts in 3rd plane gives (c + 1) pieces. Therefore a, b and c cuts in three dimensions will give (a + 1) (b + 1) (c + 1) pieces.
If number of cuts is given then maximum number of pieces can be obtain when a = b = c or these three are as close as possible while for minimum number of pieces can be obtain when all the cuts are made is in one plane.
Example- If total number of cuts is 10 then find the minimum and maximum number of pieces that can be obtained.
Solution:- When all the cuts are in one plane then total number of pieces = 11 For maximum number of pieces a = 4, b = 3 and c = 3 then total number of pieces = 5 × 4 × 4 = 80
Example-If total number of pieces are 45 then find the possible number of cuts.
Solution:- Since 45 = 1 × 1 × 45 = 1 × 3 × 15 = 1 × 9 × 5 = 3 × 3 × 5, and hence corresponding value of (a, b, c) = (0, 0, 44), (0, 2, 14), (0, 8, 4) & (2, 2, 4) and hence total number of cuts = 44, 16, 12 or 8
Removal of a corner cube: If a corner cube is removed and then all the exposed surface painted then changes due to the removal of a corner cube is as follows: (Lets take an example of 4 × 4 × 4 cube)

i. Total surface area will remain unchanged.
ii. Total number of cubes
iii. Number of cubes whose three face is painted will increase by 2 so number of such cubes is 10
iv. Number of cubes whose two face is painted will decrease by 3 so number of such cubes is 21
v. Number of cubes whose 1 face is painted will remain unchanged
vi. Number of cubes whose no face is painted will remain unchanged
Example- 343 cubes of similar size are arranged in the form of a bigger cube (7 cubes on each side, i. e., 7 × 7 × 7) and kept at the corner of a room, all the exposed surfaces are painted then:
1.How many of the cubes have 0 faces painted?
(a) 64 (b) 125 (c) 240 (d) None of these
2. How many of the cubes have 2 faces painted?
(a) 14 (b) 18 (c) 16 (d) None of these
3. How many of the cubes have at most faces painted?
(a) 208 (b) 244 (c) 342 (d) None of these
4. How many of the cubes have at least 2 faces painted?
(a) 19 (b) 144 (c) 120 (d) None of these
5. How many of the cubes have 3 faces painted?
(a) 0 (b) 3 (c) 5 (d) None of these
Solution:- Out of 6 faces of 3 faces are exposed and those were painted. Number of vertices with three faces exposed (Painted) is 1
Number of vertices with 2 faces exposed (Painted) is 3
Number of vertices with 1 faces exposed (Painted) is 3
Number of vertices with 0 faces exposed (Painted) is 1
Number of sides with 2 sides exposed (Painted) is 3
Number of sides with 1 sides exposed (Painted) is 6
Number of sides with no sides exposed (Painted) is 3
From the above observation
Number of cubes with 3 faces Painted is 1
Number of cubes with 2 faces Painted is given by sides
which is exposed from two sides and there are 3 such
sides and from one side we will get 6 such cubes hence required number of cubes is 6 × 3 = 18
Number of cubes with 1 face Painted is given by faces which is exposed from one sides and there are 3 such faces hence required number of cubes is 36 × 3 = 108
Number of cubes with 0 face Painted is given by difference between total number of cubes – number of cubes with at least 1 face painted = 343 – 1 – 18 – 108 = 216
In other words number of cubes with 0 painted is (7 – 1)3 = 216.
1.(d From the above explanation number of the cubes with 0 faces painted is 216.
2. (b) From the above explanation number of the cubes with 2 faces painted is 18.
3. (c) From the above explanation number of the cubes with at most 2 faces painted is 216 + 108 + 18 = 342. Or else 343 -1 = 342
4. (a) From the above explanation number of the cubes with at least 2 faces painted is 18 + 1 = 19.
5. (d) From the above explanation number of the cubes with 3 faces painted is 1.